��Ŀ����
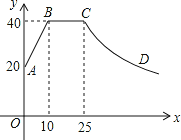
����Ŀ��(10��)��һ����ֱ�Ĺ�·��������A��B��C������ׯ���ס�������ͬʱ�ֱ��A��B�������������Ħ�г�������綯���ع�·����ʻ��C�壬���յ���C�壮��ס������˵�C��ľ���y1��y2(km)����ʻʱ��x(h)֮��ĺ�����ϵ��ͼ��ʾ����ش��������⣺

(1)A��C�����ľ���Ϊ________km��a��________��
(2)���ͼ�е�P�����꣬�����õ���������ʾ��ʵ�����壻
(3)������ʻ�����У���ʱ���10km?
���𰸡�(1)120��2����2������������3��x��![]() h��x��
h��x��![]() h��x��
h��x��![]() hʱ
hʱ
�������������������1����ͼ��֪��y�ύ��������ʾA��C�����ľ���Ϊ120km������0.5Сʱ����C��90km����ʻ120-90=30km���ٶ�Ϊ60km/h�����a=2��
��2�����y1��y2������������ʽ���������̼�����õ�P���ꣻ
��3���ɣ�2���еĺ�������ʽ�����ݾ��10km�������̣�̽�ֵó��𰸼��ɣ�
�����������1��A��C�����ľ���120km��
a=120��[��120-90����0.5]=2��
�ʴ�Ϊ��120��2��
��2����y1=k1x+120��
���루2��0���ã�0=2k1+120��
��ã�k1=-60��
����y1=-60x+120��
��y2=k2x+90��
���루3��0���ã�0=3k2+90��
��ã�k2=-30��
����y2=-30x+90��
��-60x+120=-30x+90
���x=1����y1=y2=60��
����P��1��60����
��3����y1-y2=10��
��-60x+120-��-30x+90��=10��
���x=![]() ��
��
��y2-y1=10��
��-30x+90-��-60x+120��=10��
���x=![]() ��
��
�����ߵ�C�أ����Ҿ���C��10kmʱ��
-30x+90=10��
���x=![]() ��
��
������֪��x=![]() h����x=
h����x=![]() h����x=
h����x=![]() h�Ҿ��10km��
h�Ҿ��10km��

 ��ĩ100�ִ��غ�������ϵ�д�
��ĩ100�ִ��غ�������ϵ�д� Сѧ�������Ծ�ϵ�д�
Сѧ�������Ծ�ϵ�д�