题目内容
【题目】已知抛物线
（
，且为常数）．
（
）求证：抛物线与
轴有两个公共点．
（
）若抛物线与轴的一个交点为
，另一个交点为
，与
轴交点为
，直接写出直线
与抛物线对称轴的交点
的坐标．
【答案】(1)证明见解析 （2）
【解析】
（1）令抛物线的y=x2+（a-2）x-2a的，值等于0，证所得方程x2+（a-2）x-2a=0的△>0即可；
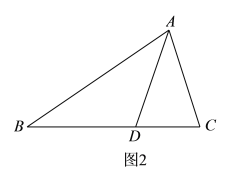
（2）由与
轴的一个交点为
，则有
，解得a=1，所以
，即
，可得B点坐标（2，0），与y轴交点
；再利用待定系数法和对称轴，即可求得解析式.
解：（
）
，
，
，
，
，
又∵
且
为常数，
∴
，
∴
，
∴抛物线与轴有两个公共点．
（
）∵与轴的一个交点为，
∴把代入
中有
，
，
．
∴，
∴，
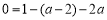∴另一个交点是
，
与轴交点，
∴设直线
为：
，
代入
，
后，
，
∴
，
又∵抛物线的对称轴是
，
∴
，
∴点．
练习册系列答案
相关题目
【题目】某公司计划投入50万元，开发并生产甲乙两种产品，根据市场调查预计甲产品的年获利y1（万元）与投入资金x（万元）成正比例，乙产品的年获利y2（万元）与投入资金x（万元）的平方成正比例，设该公司投入乙产品x（万元），两种产品的年总获利为y万元（x≥0），得到了表中的数据．
x（万元） | 20 | 30 |
y（万元） | 10 | 13 |
（1）求y与x的函数关系式；
（2）该公司至少可获得多少利润？请你利用所学的数学知识对该公司投入资金的分配提出合理化建
议，使他能获得最大利润，并求出最大利润是多少？
（3）若从年总利润扣除投入乙产品资金的a倍（a≤1）后，剩余利润随x增大而减小，求a的取值
范围．
