题目内容
如图,点E、F分别为正方形ABCD中AB、BC边的中点,连接AF、DE相交于点G,连接CG,则cos∠CGD=( )
A. B.
B.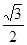 C.
C.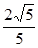 D.
D.
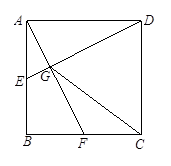
A.
 B.
B.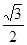 C.
C.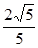 D.
D.
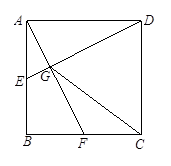
D
试题分析:把G延长交AB于H,
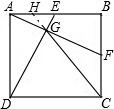
由题意可得△ADE≌△BAF
 ∠FAB=∠EDA
∠FAB=∠EDA∵∠FAB+∠DAG=90°,
∴∠EDA+∠DAG=90°,
∴AF⊥DE,
∴△AEG∽△DAG∽△DEA,
∵AE:AD=1:2,
∴EG:DG=1:4,
∵AB∥CD,
∴△HEG∽△CDG,
∴HE:CD=HG:CG=EG:DG=1:4,
∵CD=AB=2AE,
∴HE:AE=1:2,
∴H为AE的中点,
∴在Rt△AGE中,HG=
 AE,∠HEG=∠HE
AE,∠HEG=∠HE∴∠HEG=∠HGE=∠DGC
设AB=
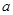 则AE=
则AE=
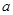 DE=
DE=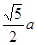
又EG:DG=1:4,
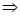 EG=
EG=
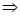 cos∠CGD=cos∠AEG=
cos∠CGD=cos∠AEG=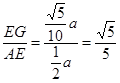

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
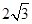 ,以AC为边在△ABC的外部作等边△ACD,连接BD.
,以AC为边在△ABC的外部作等边△ACD,连接BD.
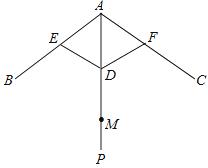
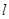 上确定点D,使CD与
上确定点D,使CD与
 ,
,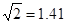 );
);
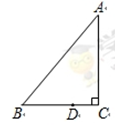
 )
)
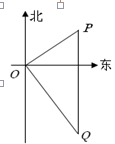
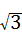 (坡比是坡面的铅直高度BC与水平宽度AC之比),则AC的长是( )
(坡比是坡面的铅直高度BC与水平宽度AC之比),则AC的长是( )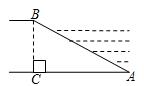
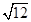 -
-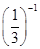 .
.