题目内容
【题目】（发现问题）
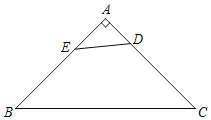
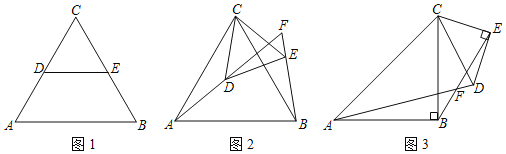
（1）如图1，已知△CAB和△CDE均为等边三角形，D在AC上，E在CB上，易得线段AD和BE的数量关系是 ．
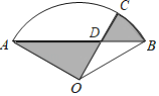
（2）将图1中的△CDE绕点C旋转到图2的位置，直线AD和直线BE交于点F．
①判断线段AD和BE的数量关系，并证明你的结论；
②图2中∠AFB的度数是 ．
（探究拓展）
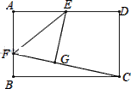
（3）如图3，若△CAB和△CDE均为等腰直角三角形，∠ABC＝∠DEC＝90°，AB＝BC，DE＝EC，直线AD和直线BE交于点F，分别写出∠AFB的度数，线段AD、BE间的数量关系．
【答案】（1）AD=BE；（2）①AD=BE，证明详见解析；②60°；（3）∠AFB=45°，AD=
BE．
【解析】
（1）由等腰三角形的性质可求解；
（2）①由“SAS”可证△ACD≌△BCE，可得AD=BE；
②由全等三角形的性质可得∠ACD＝∠CBF，即可解决问题．
（3）结论：∠AFB=45°，AD=BE．证明△ACD∽△BCE，可得
=，∠CBF=∠CAF，由此即可解决问题．
（1）∵△CAB和△CDE均为等边三角形，
∴CA=CB，CD=CE，
∴AD=BE，
故答案为：AD=BE；
（2）如图2中，
①AD=BE；
∵△ABC和△CDE均为等边三角形，
∴CA=CB，CD=CE，∠ACB=∠DCE=60°，
∴∠ACD=∠BCE，
∴△ACD≌△BCE（SAS），
∴AD=BE；
②∠AFB=60°；
∵△ACD≌△BCE，
∴∠ACD=∠CBF，
设BC交AF于点O．
∵∠AOC=∠BOF，
∴∠BFO=∠ACO=60°，
∴∠AFB=60°，
故答案为60°；
（3）结论：∠AFB=45°，AD=BE．
理由：如图3中，
∵∠ABC=∠DEC=90°，AB=BC，DE=EC，
∴∠ACD=45°+∠BCD=∠BCE，
=，
∴△ACD∽△BCE，
∴=，∠CBF=∠CAF，
∴AD=BE，
∵∠AFB+∠CBF=∠ACB+∠CAF，
∴∠AFB=∠ACB=45°．
