题目内容
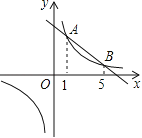
【题目】如图所示,在平面直角坐标系中,正方形OABC的顶点O与原点重合,顶点A,C分别在x轴、y轴上,双曲线y=kx﹣1(k≠0,x>0)与边AB、BC分别交于点N、F,连接ON、OF、NF.若∠NOF=45°,NF=2,则点C的坐标为_____.
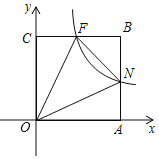
【答案】(0,![]() +1)
+1)
【解析】
将△OAN绕点O逆时针旋转90°,点N对应N′,点A对应A′,由旋转和正方形的性质即可得出点A′与点C重合,以及F、C、N′共线,通过角的计算即可得出∠N'OF=∠NOF=45°,结合ON′=ON、OF=OF即可证出△N'OF≌△NOF(SAS),由此即可得出N′M=NF=2,再由△OCF≌△OAN即可得出CF=N,通过边与边之间的关系即可得出BN=BF,利用勾股定理即可得出BN=BF=![]() ,设OC=a,则N′F=2CF=2(a﹣
,设OC=a,则N′F=2CF=2(a﹣![]() ),由此即可得出关于a的一元一次方程,解方程即可得出点C的坐标.
),由此即可得出关于a的一元一次方程,解方程即可得出点C的坐标.
将△OAN绕点O逆时针旋转90°,点N对应N′,点A对应A′,如图所示.
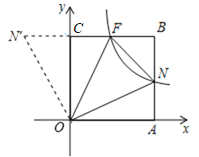
∵OA=OC,
∴OA′与OC重合,点A′与点C重合.
∵∠OCN′+∠OCF=180°,
∴F、C、N′共线.
∵∠COA=90°,∠FON=45°,
∴∠COF+∠NOA=45°.
∵△OAN旋转得到△OCN′,
∴∠NOA=∠N′OC,
∴∠COF+∠CON'=45°,
∴∠N'OF=∠NOF=45°.
在△N'OF与△NOF中,
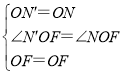 ,
,
∴△N′OF≌△NOF(SAS),
∴NF=N'F=2.
∵△OCF≌△OAN,
∴CF=AN.
又∵BC=BA,
∴BF=BN.
又∠B=90°,
∴BF2+BN2=NF2,
∴BF=BN=![]() .
.
设OC=a,则CF=AN=a﹣![]() .
.
∵△OAN旋转得到△OCN′,
∴AN=CN'=a﹣![]() ,
,
∴N'F=2(a﹣![]() ),
),
又∵N'F=2,
∴2(a﹣![]() )=2,
)=2,
解得:a=![]() +1,
+1,
∴C(0,![]() +1).
+1).
故答案是:(0,![]() +1).
+1).

【题目】某高科技产品开发公司现有员工50名,所有员工的月工资情况如下表:
员工 | 管理人员 | 普通工作人员 | |||||
人员结构 | 总经理 | 部门经理 | 科研人员 | 销售人员 | 高级技工 | 中级技工 | 勤杂工 |
员工数(名) | 1 | 3 | 2 | 3 | 24 | 1 | |
每人月工资(元) | 21000 | 8400 | 2025 | 2200 | 1800 | 1600 | 950 |
请你根据上述内容,解答下列问题:
(1)该公司“高级技工”有 名;
(2)所有员工月工资的平均数x为2500元,中位数为 元,众数为 元;
(3)小张到这家公司应聘普通工作人员.请你回答右图中小张的问题,并指出用(2)中的哪个数据向小张介绍员工的月工资实际水平更合理些;
(4)去掉四个管理人员的工资后,请你计算出其他员工的月平均工资![]() (结果保留整数),并判断
(结果保留整数),并判断![]() 能否反映该公司员工的月工资实际水平.
能否反映该公司员工的月工资实际水平.