题目内容
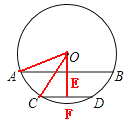
【题目】如图,⊙O的半径为17cm,弦AB∥CD,AB=30cm,CD=16cm,圆心O位于AB,CD的上方,求AB和CD的距离.

【答案】7cm.
【解析】试题分析:过点O作弦AB的垂线,垂足为E,延长AE交CD于点F,连接OA,OC;由于AB∥CD,则OF⊥CD,EF即为AB、CD间的距离;由垂径定理,易求得AE、CF的长,在构建的直角三角形中,根据勾股定理即可求出OE、OF的长,也就求出了EF的长,即弦AB、CD间的距离.
试题解析:过点O作弦AB的垂线,垂足为E,延长OE交CD于点F,连接OA,OC,
∵AB∥CD,
∴OF⊥CD,
∵AB=30cm,CD=16cm,
∴AE=![]() AB=
AB=![]() ×30=15cm,CF=
×30=15cm,CF=![]() CD=
CD=![]() ×16=8cm,
×16=8cm,
在Rt△AOE中,
OE=![]() cm,
cm,
在Rt△OCF中,
OF=![]() cm,
cm,
∴EF=OF-OE=15-8=7cm.
答:AB和CD的距离为7cm.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】小明到某服装专卖店去做社会调查,了解到该专卖店为了微励营业员的工作积极性,实行“月总收入=基本工资(固定)+计付奖金”的方法计算薪资,并获得如下信息;
营业员 | 小张 | 小王 |
月销售件数 | 200 | 150 |
月总收入/元 | 1400 | 1250 |
销售每件奖励a元,晋业员月基本工资为b元.
(1)列方程组求a,b的值.
(2)假设月销售件数为x,月总收入为y元,请写出y与x的函数关系式,并求出营业员小张上个月总收入是1700元时,小张上个月卖了多少件服装?