题目内容
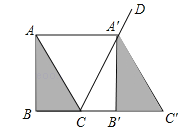
【题目】如图,将△ABC沿着射线BC方向平移至△A'B'C',使点A'落在∠ACB的外角平分线CD上,连结AA'.
(1)判断四边形ACC'A'的形状,并说明理由;
(2)在△ABC中,∠B=90°,A B=24,cos∠BAC=![]() ,求CB'的长.
,求CB'的长.

【答案】(1)四边形ACC'A'是菱形;(2)16.
【解析】试题分析:(1)根据平行四边形的判定定理(有一组对边平行且相等的四边形是平四边形)推知四边形ACC'A'是平行四边形.又对角线平分对角的平行四边形是菱形推知四边形ACC'A'是菱形.
(2)通过解直角△ABC得到AC、BC的长度,由(1)中菱形ACC'A'的性质推知AC=AA′,由平移的性质得到四边形ABB′A′是平行四边形,则AA′=BB′,所以CB′=BB′﹣BC.
试题解析:(1)四边形ACC'A'是菱形.理由如下:
由平移的性质得到:AC∥A′C′,且AC=A′C′,则四边形ACC'A'是平行四边形,∴∠ACC′=∠AA′C′,又∵CD平分∠ACB的外角,即CD平分∠ACC′,∴CD也平分∠AA′C′,∴四边形ACC'A'是菱形.
(2)∵在△ABC中,∠B=90°,A B=24,cos∠BAC=![]() ,
,
∴cos∠BAC=![]() =
=![]() ,即
,即![]() =
=![]() ,∴AC=26,
,∴AC=26,
∴由勾股定理知:BC=![]() =
=![]() =10,
=10,
又由(1)知,四边形ACC'A'是菱形,∴AC=AA′=26,
由平移的性质得到:AB∥A′B′,AB=A′B′,则四边形ABB′A′是平行四边形,
∴AA′=BB′=26,∴CB′=BB′﹣BC=16.

 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案【题目】为了解某种车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来, 制成如表:
汽车行驶时间 t(小时) | 0 | 1 | 2 | 3 | … |
油箱剩余油量 Q(升) | 100 | 94 | 88 | 82 | … |
(1)上表反映的两个变量中,自变量是 ,因变量是 ;
(2)根据上表可知,该车油箱的大小为 升,每小时耗油 升;
(3)请求出两个变量之间的关系式(用 t 来表示 Q).
【题目】某公司有A、B两种客车,它们的载客量和租金如下表,星星中学根据实际情况,计划用A、B型车共5辆,同时送七年级师生到校基地参加社会实践活动.
A | B | |
载客量(人/辆) | 40 | 20 |
租金(元/辆) | 200 | 150 |
(1)若要保证租金费用不超过980元,请问该学校有哪几种租车方案?
(2)在(1)的条件下,若七年级师生共有150人,问哪种租车方案最省钱?

