题目内容
如图,抛物线y=-x2+ax+b与x轴交于A、B两点,交y轴于点C,且∠BAC=α,∠ABC=β,ta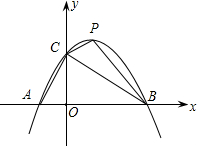 nα-tanβ=2,∠ACB=90°.
nα-tanβ=2,∠ACB=90°.①求抛物线的解析式;
②若抛物线顶点为P,求S四边形ABPC.
分析:(1)可先求得点C的坐标,再别表示出tanα、tanβ的值,根据两者的等量关系及韦达定理即可求得a的值,从而确定二次函数的解析式.
(2)由抛物线的解析式,可求得P点坐标,进而可求得直线PC的解析式,延长PC交x轴于D,根据直线PC的解析式即可得到D点的坐标,那么四边形ABPC的面积即可由△PDB和△ADC的面积差求得.
(2)由抛物线的解析式,可求得P点坐标,进而可求得直线PC的解析式,延长PC交x轴于D,根据直线PC的解析式即可得到D点的坐标,那么四边形ABPC的面积即可由△PDB和△ADC的面积差求得.
解答: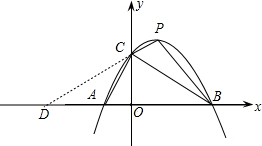 解:(1)根据题意设点A(x1,O)、点B(x2,O),且C(O,b);
解:(1)根据题意设点A(x1,O)、点B(x2,O),且C(O,b);
x1<0,x2>0,b>0,
∵x1,x2是方程-x2+ax+b=0的两根,
∴x1+x2=a,x1•x2=-b;
在Rt△ABC中,OC⊥AB,
∴OC2=OA•OB,
∵OA=-x1,OB=x2,
∴b2=-x1•x2=b,
∵b>0,
∴b=1,
∴C(0,1).
在Rt△AOC和Rt△BOC中,
tanα-tanβ=
-
=-
-
=-
=
=2,(4分)
∴a=2,
∴抛物线解析式为:y=-x2+2x+1;(5分)
(2)∵y=-x2+2x+1,
∴顶点P的坐标为(1,2),
当-x2+2x+1=0时,x=1±
,
∴A(1-
,0),B(1+
,0),(6分)
延长PC交x轴于点D,过C、P的直线为y=x+1,
∴点D的坐标为(-1,0),(7分)
S四边形ABPC=S△DPB-S△DCA
=
•|DB|•yp -
•|AD|•yc
=
×(2+
)×2-
×(2-
)×1
=
.
 解:(1)根据题意设点A(x1,O)、点B(x2,O),且C(O,b);
解:(1)根据题意设点A(x1,O)、点B(x2,O),且C(O,b);x1<0,x2>0,b>0,
∵x1,x2是方程-x2+ax+b=0的两根,
∴x1+x2=a,x1•x2=-b;
在Rt△ABC中,OC⊥AB,
∴OC2=OA•OB,
∵OA=-x1,OB=x2,
∴b2=-x1•x2=b,
∵b>0,
∴b=1,
∴C(0,1).
在Rt△AOC和Rt△BOC中,
tanα-tanβ=
| OC |
| OA |
| OC |
| OB |
| 1 |
| x1 |
| 1 |
| x2 |
| x1+x2 |
| x1x2 |
| a |
| b |
∴a=2,
∴抛物线解析式为:y=-x2+2x+1;(5分)
(2)∵y=-x2+2x+1,
∴顶点P的坐标为(1,2),
当-x2+2x+1=0时,x=1±
| 2 |
∴A(1-
| 2 |
| 2 |
延长PC交x轴于点D,过C、P的直线为y=x+1,
∴点D的坐标为(-1,0),(7分)
S四边形ABPC=S△DPB-S△DCA
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
=
2+3
| ||
| 2 |
点评:本题考查二次函数的综合运用,本题涉及到了直角三角形的性质、根与系数的关系、锐角三角形函数、二次函数解析式的确定以及图形面积的求法,当所求图形不规则或无法直接求出其面积时,一般将其转化成其他规则图形的面积的和差来解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
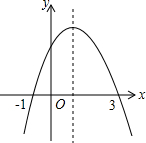 如图,抛物线y=ax2+bx+c(a≠0)与x轴两交点是A(-1,0),B(3,0),则如图可知y<0时,x的取值范围是( )
如图,抛物线y=ax2+bx+c(a≠0)与x轴两交点是A(-1,0),B(3,0),则如图可知y<0时,x的取值范围是( )| A、-1<x<3 | B、3<x<-1 | C、x>-1或x<3 | D、x<-1或x>3 |
 26、已知:如图,抛物线C1,C2关于x轴对称;抛物线C1,C3关于y轴对称.抛物线C1,C2,C3与x轴相交于A、B、C、D四点;与y相交于E、F两点;H、G、M分别为抛物线C1,C2,C3的顶点.HN垂直于x轴,垂足为N,且|OE|>|HN|,|AB|≠|HG|
26、已知:如图,抛物线C1,C2关于x轴对称;抛物线C1,C3关于y轴对称.抛物线C1,C2,C3与x轴相交于A、B、C、D四点;与y相交于E、F两点;H、G、M分别为抛物线C1,C2,C3的顶点.HN垂直于x轴,垂足为N,且|OE|>|HN|,|AB|≠|HG|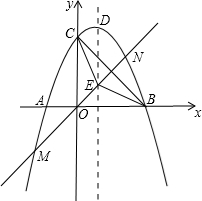 如图,抛物线交x轴于点A(-2,0),点B(4,0),交y轴于点C(0,4).
如图,抛物线交x轴于点A(-2,0),点B(4,0),交y轴于点C(0,4).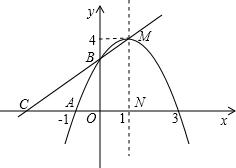 以P为圆心的圆经过点A,并且与直线BM相切?若存在,求出点P的坐标;若不存在,请说明理由.
以P为圆心的圆经过点A,并且与直线BM相切?若存在,求出点P的坐标;若不存在,请说明理由.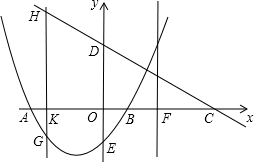 .点C是点A关于点B的对称点,点F是线段BC的中点,直线l过点F且与y轴平行.直线y=-x+m过点C,交y轴于D点.
.点C是点A关于点B的对称点,点F是线段BC的中点,直线l过点F且与y轴平行.直线y=-x+m过点C,交y轴于D点.