Question

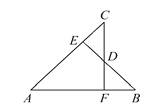
【题目】在锐角三角形ABC中，AH是BC边上的高，分别以AB，AC为一边，向外作正方形ABDE和ACFG，连接CE，BG和EG，EG与HA的延长线交于点M，下列结论：①BG=CE；②BG⊥CE；③AM是△AEG的中线；④∠EAM=∠ABC，其中正确结论的个数是（ ）

A. 4个 B. 3个 C. 2个 D. 1个

Answer 1

【答案】A

【解析】试题分析：根据正方形的性质可得AB=AE，AC=AG，∠BAE=∠CAG=90°，然后求出∠CAE=∠BAG，再利用“边角边”证明△ABG和△AEC全等，根据全等三角形对应边相等可得BG=CE，判定①正确；设BG、CE相交于点N，根据全等三角形对应角相等可得∠ACE=∠AGB，然后求出∠CNG=90°，根据垂直的定义可得BG⊥CE，判定②正确；过点E作EP⊥HA的延长线于P，过点G作GQ⊥AM于Q，根据同角的余角相等求出∠ABH=∠EAP，再利用“角角边”证明△ABH和△EAP全等，根据全等三角形对应角相等可得∠EAM=∠ABC判定④正确，全等三角形对应边相等可得EP=AH，同理可证GQ=AH，从而得到EP=GQ，再利用“角角边”证明△EPM和△GQM全等，根据全等三角形对应边相等可得EM=GM，从而得到AM是△AEG的中线，故③正确. 综上所述，①②③④结论都正确．

故选：A．