��Ŀ����
����•һ�����ڣ�ij����վ�ÿ��������������ÿ�������Ҫ��ʱ���ŶӵȺ��Ʊ�������鷢�֣��ڳ�վ��ʼ��Ʊʱ����640���ŶӼ�Ʊ����Ʊ��ʼ�������ÿͼ���ǰ���ŶӼ�Ʊ��վ�����ÿͰ��̶����ٶ����ӣ���Ʊ�ڼ�Ʊ���ٶ�Ҳ�ǹ̶��ģ���Ʊʱ��ÿ���Ӻ��������ŶӼ�Ʊ��վ16�ˣ�ÿ����ÿ����Ʊ�ڼ�Ʊ14�ˣ���֪��Ʊ��ǰa����ֻ������������Ʊ�ڣ�ijһ������ŶӵȺ��Ʊ������y���ˣ����Ʊʱ��x�����ӣ��Ĺ�ϵ��ͼ��ʾ��

��1����a��ֵ��
��2�����Ʊ����20����ʱ�������ŶӵȺ��Ʊ���ÿ�������
��3����Ҫ�ڿ�ʼ��Ʊ��15�������������Ŷӵ��ÿͶ��ܼ�Ʊ��վ���Ա������վ���ÿ��浽��죬�ʼ�Ʊһ��ʼ������Ҫͬʱ���ż�����Ʊ�ڣ�

��1����a��ֵ��
��2�����Ʊ����20����ʱ�������ŶӵȺ��Ʊ���ÿ�������
��3����Ҫ�ڿ�ʼ��Ʊ��15�������������Ŷӵ��ÿͶ��ܼ�Ʊ��վ���Ա������վ���ÿ��浽��죬�ʼ�Ʊһ��ʼ������Ҫͬʱ���ż�����Ʊ�ڣ�
��1��a=10��2��260�ˣ�3��5����Ʊ��
�⣺��1����ͼ��֪��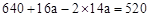 ��
��
��a=10��
��2���赱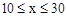 ʱ��y��x֮��ĺ�����ϵʽΪy=kx+b�������⣬��
ʱ��y��x֮��ĺ�����ϵʽΪy=kx+b�������⣬��
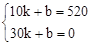 ����ã�
����ã�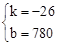 ��
��
��y=��26x+780��
��x=2ʱ��y=260������Ʊ����20����ʱ�������ŶӵȺ��Ʊ���ÿ���260�ˡ�
��3������ͬʱ����n����Ʊ�ڣ���������֪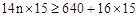 ��
��
��ã�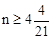 ��
��
��n��������n=5��
��������Ҫͬʱ����5����Ʊ�ڣ�
��1������ԭ�е�������a���Ӽ�Ʊ������+a�������ӵ�����=520��������������Ϳ��ԡ�
��2���赱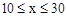 ʱ��y��x֮��ĺ�����ϵʽΪy=kx+b���ɴ���ϵ������������Ľ���ʽ���ٽ�x=20�������ʽ�Ϳ���������ۡ�
ʱ��y��x֮��ĺ�����ϵʽΪy=kx+b���ɴ���ϵ������������Ľ���ʽ���ٽ�x=20�������ʽ�Ϳ���������ۡ�
��3������ͬʱ����n����Ʊ�ڣ�����ԭ��������+15�ֽ�վ������n����Ʊ��15���Ӽ�Ʊ������������ʽ�������⼴�ɡ���
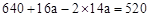 ��
����a=10��
��2���赱
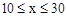 ʱ��y��x֮��ĺ�����ϵʽΪy=kx+b�������⣬��
ʱ��y��x֮��ĺ�����ϵʽΪy=kx+b�������⣬��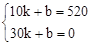 ����ã�
����ã�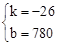 ��
����y=��26x+780��
��x=2ʱ��y=260������Ʊ����20����ʱ�������ŶӵȺ��Ʊ���ÿ���260�ˡ�
��3������ͬʱ����n����Ʊ�ڣ���������֪
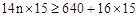 ��
����ã�
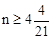 ��
����n��������n=5��
��������Ҫͬʱ����5����Ʊ�ڣ�
��1������ԭ�е�������a���Ӽ�Ʊ������+a�������ӵ�����=520��������������Ϳ��ԡ�
��2���赱
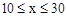 ʱ��y��x֮��ĺ�����ϵʽΪy=kx+b���ɴ���ϵ������������Ľ���ʽ���ٽ�x=20�������ʽ�Ϳ���������ۡ�
ʱ��y��x֮��ĺ�����ϵʽΪy=kx+b���ɴ���ϵ������������Ľ���ʽ���ٽ�x=20�������ʽ�Ϳ���������ۡ���3������ͬʱ����n����Ʊ�ڣ�����ԭ��������+15�ֽ�վ������n����Ʊ��15���Ӽ�Ʊ������������ʽ�������⼴�ɡ���

��ϰ��ϵ�д�
 ����νӽ̲���ĩ���Ԥϰ�人������ϵ�д�
����νӽ̲���ĩ���Ԥϰ�人������ϵ�д� ������ҵ��ٳɳ����½������������ϵ�д�
������ҵ��ٳɳ����½������������ϵ�д�
�����Ŀ
 ��ͼ����һ���������ڵ�A��B���㣬ֱ��AB��x�ύ�ڵ�C����B������Ϊ����6��n�����߶�OA=5��EΪx����������һ�㣬��tan��AOE=
��ͼ����һ���������ڵ�A��B���㣬ֱ��AB��x�ύ�ڵ�C����B������Ϊ����6��n�����߶�OA=5��EΪx����������һ�㣬��tan��AOE=

 ��0)���㣬��ʽ0��kx��b����x�Ľ⼯Ϊ_ ��
��0)���㣬��ʽ0��kx��b����x�Ľ⼯Ϊ_ ��




 �����������ʱ��t��Сʱ���ĺ���ͼ�����Ѳ��ͧԭ�ƻ��㵽���ʱ���� .
�����������ʱ��t��Сʱ���ĺ���ͼ�����Ѳ��ͧԭ�ƻ��㵽���ʱ���� .

 ��������ֱ���
��������ֱ��� ���㣬����
���㣬���� ͬʱ��
ͬʱ�� �������ͬʱ����
�������ͬʱ����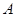 �㣬�˶�ֹͣ����
�㣬�˶�ֹͣ���� ���߶�
���߶� �˶����ٶ�Ϊÿ��1����λ���ȣ���
�˶����ٶ�Ϊÿ��1����λ���ȣ��� ��·��
��·�� ��
��
 �룬
�룬 �����Ϊ
�����Ϊ �����
����� ʱ�������
ʱ������� Ϊ�����ƽ���ı��εĵ��ĸ�����
Ϊ�����ƽ���ı��εĵ��ĸ�����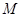 �����꣮
�����꣮