题目内容
某大学生利用暑假40天社会实践参与了一家网店经营,了解到一种成本为20元/件的新型商品在第x天销售的相关信息如下表所示。
(1)请计算第几天该商品的销售单价为35元/件?
(2)求该网店第x天获得的利润y关于x的函数关系式。
(3)这40天中该网店第几天获得的利润最大?最大利润是多少?
| 销售量p(件) | P=50—x |
| 销售单价q(元/件) | 当1≤x≤20时, 当21≤x≤40时,  |
(2)求该网店第x天获得的利润y关于x的函数关系式。
(3)这40天中该网店第几天获得的利润最大?最大利润是多少?
(1)第10天或第25天该商品的销售单价为35元/件(2) (3)这40天中该网店第21天获得的利润最大?最大利润是725元
(3)这40天中该网店第21天获得的利润最大?最大利润是725元
 (3)这40天中该网店第21天获得的利润最大?最大利润是725元
(3)这40天中该网店第21天获得的利润最大?最大利润是725元解:(1)当1≤x≤20时,令 ,解得;
,解得; ;
;
当21≤x≤40时,令 ,解得;
,解得; 。
。
∴第10天或第25天该商品的销售单价为35元/件。
(2)当1≤x≤20时, ;
;
当21≤x≤40时, 。
。
∴y关于x的函数关系式为 。
。
(3)当1≤x≤20时, ,
,
∵ ,∴当x=15时,y有最大值y1,且y1=612.5。
,∴当x=15时,y有最大值y1,且y1=612.5。
当21≤x≤40时,∵26250>0,∴ 随着x的增大而减小,
随着x的增大而减小,
∴当x=21时, 有最大值y2,且
有最大值y2,且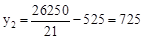 。
。
∵y1<y2,
∴这40天中该网店第21天获得的利润最大?最大利润是725元。
(1)分别将q=35代入销售单价关于x的函数关系式,求出x即可。
(2)应用利润=销售收入-销售成本列式即可。
(3)应用二次函数和反比例函数的性质,分别求出最大值比较即得所求。
 ,解得;
,解得; ;
;当21≤x≤40时,令
 ,解得;
,解得; 。
。∴第10天或第25天该商品的销售单价为35元/件。
(2)当1≤x≤20时,
 ;
;当21≤x≤40时,
 。
。∴y关于x的函数关系式为
 。
。(3)当1≤x≤20时,
 ,
,∵
 ,∴当x=15时,y有最大值y1,且y1=612.5。
,∴当x=15时,y有最大值y1,且y1=612.5。当21≤x≤40时,∵26250>0,∴
 随着x的增大而减小,
随着x的增大而减小,∴当x=21时,
 有最大值y2,且
有最大值y2,且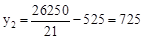 。
。∵y1<y2,
∴这40天中该网店第21天获得的利润最大?最大利润是725元。
(1)分别将q=35代入销售单价关于x的函数关系式,求出x即可。
(2)应用利润=销售收入-销售成本列式即可。
(3)应用二次函数和反比例函数的性质,分别求出最大值比较即得所求。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 交x轴于点A,交y轴于点B,BD平分∠AB0,点C是x轴的正半轴上一点,连接BC,且AC=AB.
交x轴于点A,交y轴于点B,BD平分∠AB0,点C是x轴的正半轴上一点,连接BC,且AC=AB.
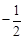

 的图象与反比例函数
的图象与反比例函数 在第一象限内的图象交于点A,与x轴交于点B,线段OA=5,C为x轴正半轴上一点,且
在第一象限内的图象交于点A,与x轴交于点B,线段OA=5,C为x轴正半轴上一点,且 .
.


 时,余油量Q的值为 ;
时,余油量Q的值为 ; 交于点A(-1,-5)、D(5,1),并分别与x轴、y轴交于点C、B.
交于点A(-1,-5)、D(5,1),并分别与x轴、y轴交于点C、B.
 (k≠0)的图象的大致位置是( )
(k≠0)的图象的大致位置是( )