Question

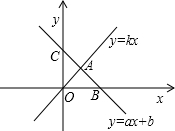
已知直线y₁=2x-6与y₂=-ax+6在x轴上交于点A，直线y=x与y₁，y₂分别交于C，B两点．
（1）求a的值；
（2）求三条直线所围成的△ABC的面积．

Answer 1

（1）令y=0，则2x-6=0，
解得x=3，
所以，点A（3，0），
把点A的坐标代入y₂=-ax+6得，-3a+6=0，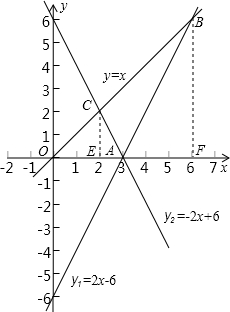
解得a=2；

（2）联立

y=x y=2x-6

，
解得

x=6 y=6

，
所以，点C（6，6），
联立

y=x y=-2x+6

，
解得

x=2 y=2

，
所以，点B（2，2），
如图，过点B作BF⊥x轴于F，过点C作CE⊥x轴于E，
则△ABC的面积=

1

2

（2+6）×（6-2）-

1

2

×（3-2）×2-

1

2

×（6-3）×6，
=16-1-9，
=16-10，
=6．