��Ŀ����
����Ŀ�������龳����ͼ1����D�ǡ�ABC���һ�㣬��E��BC�ߵ��ӳ����ϣ�BDƽ�֡�ABC��CDƽ�֡�ACE����̽����D���A��������ϵ��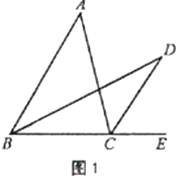
��1������̽����
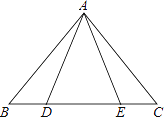
��ͼ2������ABC�ǵȱ������Σ������������䣬���D����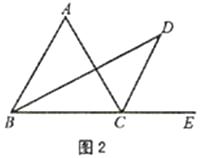
��ͼ3������ABC�ǵ��������Σ����ǡ�A��100�㣬�����������䣬���D����������ͼ�У���D���A�����ı�����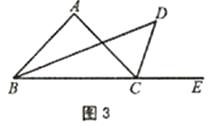
��2������֤����
��ͼ1����ABCΪһ�������Σ��ڣ�1���л�õġ�D���A�Ĺ�ϵ�Ƿ�����������������ͼ1֤����Ľ��ۣ�����������˵�����ɣ�
���𰸡�
��1��30�㣻50�㣻1��2
��2���⣺����.
��BDƽ�֡�ABC��
���ABD=��DBC��
��CDƽ�֡�ACE��
���ACD=��DCE��
�ߡ�ACE�ǡ�ABC����ǣ�
���ACE=��ABC����A�� ��2��DCE =2��DBC+��A��
�ߡ�DCE�ǡ�BCD����ǣ�
���DCE����DBC����D��
��2��DBC+��A��2����DBC����D����
���D�� ![]() ��A������D����A��1:2
��A������D����A��1:2
���������⣺(1)��30��50��1��2�� (1���ٸ��ݽ�ƽ���ߵĶ���ó���ABD=��DBC=30�㣬��ACD=��DCE=60�㣬���������ε���Ƕ����ó���DCE=��DBC+��D ,�Ӷ��ó���D=30�� ;�ڸ��ݵ��������ε����ʵó���ABC=40�� ,���ݽ�ƽ���ߵĶ���ó���ABD=��DBC=20��,���������ε���Ƕ����ó���ACE=��A����ABC��140�� ,��ACD=��DCE=70�� ,���������ε���Ƕ����ó���DCE=��DBC+��D ,�Ӷ��ó���D=50�� ;
(2�����ݽ�ƽ���ߵĶ���ó���ABD=��DBC����ACD=��DCE�����������ε���Ƕ����ó���ACE=��ABC����A�� ��2��DCE =2��DBC+��A����DCE����DBC����D���Ӷ��ó�2��DBC+��A��2����DBC����D��������D����A��1:2 ��

����Ŀ���Թ���ʵ��һϵ������ũ���Ż����ߺ�ũ�������������ӣ�ij������Ͻ��ׯȥ������˾����루��λ��Ԫ����������
���˾����� | 10500 | 10700 | 10800 | 10900 | 11500 |
��ׯ���� | 1 | 1 | 3 | 3 | 1 |
����ȥ�����ׯ���˾��������λ���ǣ�������
A. 10700 B. 10800 C. 10850 D. 10900