Question

【题目】如图，已知平面直角坐标系中，直线 与x轴交于点A，与y轴交于B，与直线y＝x交于点C．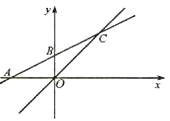

（1）求A、B、C三点的坐标；
（2）求△AOC的面积；
（3）已知点P是x轴正半轴上的一点，若△COP是等腰三角形，直接写点P的坐标．

Answer 1

【答案】
（1）解：当x=0得y=2，则B（0，2），当y=0得x=-4，则A（-4，0），
由于C是两直线交点，联立直线解析式为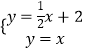
解得：
则点C的坐标为（4，4） .
（2）解：过点C作CD⊥x轴与点D
∴AO=4，CD=4
∴ = AO·CD= ×4×4=8
（3）解：点P的坐标为（4，0）或（8，0）或（ ，0）
【解析】 (1）把x=0代入 y = x + 2得出，y=2，从而得出B点的坐标，把y=0代入 y = x + 2得出，x=-4，从而得出A点的坐标，由于C是两直线交点，联立直线解析式 y = x + 2与y＝x ，解方程组得出方程组的解，即得出了C点的坐标；
（2）过点C作CD⊥x轴与点D ，根据A,C两点的坐标得出AO=4，CD=4 ，根据 S △ A O C = AO·CD，算出答案；
（3）以点O为圆心，OC长为半径，画弧，交x的正半轴于点P,根据题意OP=OC=4,从而得到P点的坐标为（4 ，0）；以点C为圆心，OC长为半径，画弧，交x的正半轴于点P,根据题意CP=OC=4,从而得到P点的坐标为(8,0) ,作OC的垂直平分线，角x的正半轴于点P，则，点P的坐标为（4,0） 。