Question

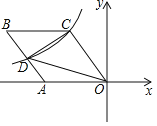
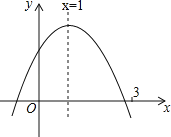
【题目】如图，二次函数y＝﹣x2+x+6与x轴相交A，B两点，与y轴相交于点C．

（1）若点E为线段BC上一动点，过点E作x轴的垂线与抛物线交于点P，垂足为F，当PE﹣2EF取得最大值时，在抛物线y的对称轴上找点M，在x轴上找点N，使得PM+MN+NB的和最小，若存在，求出该最小值及点N的坐标；若不存在，请说明理由．

（2）在（1）的条件下，若点P′为点P关于x轴的对称点，将抛物线y沿射线BP′的方向平移得到新的抛物线y′，当y′经过点A时停止平移，将△BCN沿CN边翻折，点B的对应点为点B′，B′C与x轴交于点K，若抛物线y′的对称轴上有点R，在平画内有点S，是否存在点R、S使得以K、B′、R、S为顶点的四边形是菱形，若存在，直接写出点S的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）点H（9，﹣3），PM+MN+NB的和最小值为9；（2）（，﹣）或（﹣，）；

【解析】

（1）过点B作直线HB与x轴的夹角为45°，则直线HB的表达式为：y＝x﹣12，过点C作CH⊥BH于点H，交函数对称轴于点M，交x轴于点N，则点N为所求，即可求解；

（2）分B′K为菱形的一条边、B′K为菱形的一条对角线两种情况，分别求解即可．

解：（1）二次函数y＝﹣x2+x+6与x轴相交A，B两点，与y轴相交于点C，

则点A、B、C的坐标分别为：（﹣3，0）、（12，0）、（0，6），

则直线BC的表达式为：y＝﹣x+6，

设点P（x，﹣x2+x+6），则点E（x，﹣x+6），

PE﹣2EF＝yP﹣3yE＝﹣x2+x+6﹣3（﹣x+6）＝﹣x2+3x﹣12，

当x＝9时，PE﹣2EF有最大值，此时，点P（9，6），

即点C是点P关于函数对称轴的对称点，

过点B作直线HB与x轴的夹角为45°，则直线HB的表达式为：y＝x﹣12…①，

过点C作CH⊥BH于点H，交函数对称轴于点M，交x轴于点N，则点N为所求，

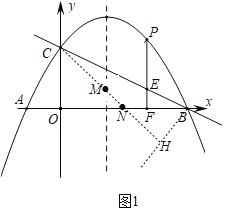
BH＝BN，PM+MN+NB的和最小值＝CM+MN+NH＝CH即为最小值，

同理直线CH的表达式为：y＝﹣x+6…②，

当y＝0时，x＝6，故点N（6，0），

联立①②并解得：x＝9，故点H（9，﹣3），

PM+MN+NB的和最小值＝CH＝ ＝9；

（2）存在，理由：

y＝﹣x2+x+6＝﹣（x﹣）2+，

点P（9，6），则点P′（9，﹣6），

则直线BP′表达式中的k值为：2，

设抛物线向左平移m个单位，则向下平移2m个单位，

则y′＝﹣（x﹣+m）2++2m，

将点A的坐标代入上式并解得：m＝3，

则y′＝﹣x2+x+3，令y′＝0，则x＝﹣3或6，故点N（6，0），

函数的对称轴为：x＝，

同理可得：直线CN的表达式为：y＝﹣x+6，直线BB′的表达式为：y＝x﹣12，

联立上述两式并解得：x＝9，

即交点坐标为：（9，﹣3），该点是点B（12，0）和点B′的中点，

由中点公式可得：点B′（6，﹣6），

同理可得：直线CB′的表达式为：y＝﹣2x+6，令y＝0，则x＝3，故点K（3，0），

设点S（m，n），点R（，s），而点B′、K的坐标分别为：（12，0）、（3，0）；

①当B′K为菱形的一条边时，

点K向右平移3个单位向下平移6个单位得到B′，

同样，点R（S）向右平移3个单位向下平移6个单位得到S（R），

即+3＝m，s﹣6＝n或﹣3＝m，s+6＝n，且KR＝B′R，即（6﹣）2+（s+6）2＝（）2+s2，

解得：m＝或﹣，n＝﹣或，

即点S的坐标为：（，﹣）或（﹣，）；

②当B′K为菱形的一条对角线时，

由中点公式得：6+3＝m+，s﹣6＝n，且KR＝B′R，

即（6﹣）2+（s+6）2＝（）2+s2，

解得：m＝，故点P（，﹣）．