题目内容
已知二次函数y=-x2+2mx-(m2+4m-8),m为正整数,它的图象与x轴交于点A、B两点(A点在B点左侧).(1)求二次函数的解析式,并画出草图;
(2)求以A,B为圆心,分别以OA、OB为半径的⊙A、⊙B异于y轴的一条外公切线的解析式;
(3)求(2)中⊙A、⊙B的外部与一条公切线围成的图形的面积.
【答案】分析:(1)根据二次函数图象与x轴有两个交点,可得判别式△≥0,列式求出m的取值范围,再根据m是正整数即可求出m的值,然后代入整理即可得到函数解析式,求出二次函数图象与x轴、y轴的交点坐标,以及对称轴,作出图象即可;
(2)根据两圆半径的关系可以求出过公切线切点的半径与x轴的夹角是60°,然后求出两切点的坐标,再根据待定系数法即可求出公切线的解析式;
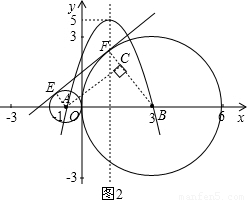
(3)如图2,先求出公切线段的长度,然后求出直角梯形ABFE的面积,再根据所求面积等于梯形ABFE的面积减去两个扇形的面积计算即可求解.
解答: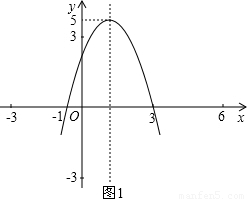 解:(1)△=(2m)2-4×(-1)×[-(m2+4m-8)],
解:(1)△=(2m)2-4×(-1)×[-(m2+4m-8)],
=-16m+32,
∵图象与x轴交于点A、B两点(A点在B点左侧),
∴△>0,
即-16m+32>0,
解得m<2,
∵m为正整数,
∴m=1,
∴y=-x2+2mx-(m2+4m-8)=-x2+2×1-(12+4×1-8)=-x2+2x+3,
即二次函数的解析式为:y=-x2+2x+3;图象如图1所示;
(2)如图2所示,当y=0时,-x2+2x+3=0,
解得x1=-1,x2=3,
点A、B的坐标是A(-1,0),B(3,0),
∴AB=1+3=4,BC=3-1=2,
∴∠BAC=30°,
∴∠ABC=90°-30°=60°,
∵1×cos60°= ,1×sin60°=
,1×sin60°= ,-1-
,-1- =-
=- ,
,
3×cos60°=3× =
= ,3×sin60°=3×
,3×sin60°=3×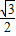 =
=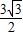 ,3-
,3- =
= ,
,
∴点E、F的坐标分别是E(- ,
,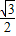 ),F(
),F( ,
, ),
),
设公切线EF的解析式是:y=kx+b,
则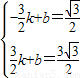 ,
,
解得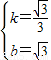 ,
,
∴公切线的解析式是y=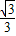 x+
x+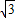 ,
,
同理在x轴下方的公切线的解析式是y=-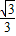 x-
x-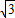 ;
;
(3)如图2,EF=AC=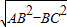 =
=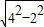 =2
=2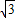 ,
,
∴梯形ABFE的面积= ×(1+3)×2
×(1+3)×2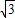 =4
=4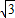 ,
,
∵∠BAC=30°,
∴∠EAO=30°+90°=120°,
∴S扇形EAO=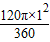 =
=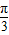 ,S扇形FBO=
,S扇形FBO=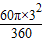 =
=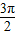 ,
,
围成的图形的面积=S梯形ABFE-S扇形EAO-S扇形FBO=4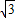 -
-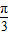 -
-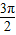 =4
=4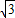 -
-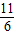 π.
π.
故答案为:(1)y=-x2+2x+3,(2)y=-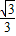 x-
x-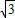 ,(3)4
,(3)4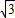 -
-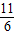 π.
π.
点评:本题综合考查了二次函数的问题,根的判别式,二次函数图象与x轴的交点问题,两圆相交的公切线解析式的求解,待定系数法求直线解析式,勾股定理,扇形的面积以及梯形的面积的求解,综合性较强,难度较大,但只要仔细分析也不难解决.
(2)根据两圆半径的关系可以求出过公切线切点的半径与x轴的夹角是60°,然后求出两切点的坐标,再根据待定系数法即可求出公切线的解析式;
(3)如图2,先求出公切线段的长度,然后求出直角梯形ABFE的面积,再根据所求面积等于梯形ABFE的面积减去两个扇形的面积计算即可求解.
解答:
 解:(1)△=(2m)2-4×(-1)×[-(m2+4m-8)],
解:(1)△=(2m)2-4×(-1)×[-(m2+4m-8)],=-16m+32,
∵图象与x轴交于点A、B两点(A点在B点左侧),
∴△>0,
即-16m+32>0,
解得m<2,
∵m为正整数,
∴m=1,
∴y=-x2+2mx-(m2+4m-8)=-x2+2×1-(12+4×1-8)=-x2+2x+3,
即二次函数的解析式为:y=-x2+2x+3;图象如图1所示;
(2)如图2所示,当y=0时,-x2+2x+3=0,
解得x1=-1,x2=3,
点A、B的坐标是A(-1,0),B(3,0),
∴AB=1+3=4,BC=3-1=2,
∴∠BAC=30°,
∴∠ABC=90°-30°=60°,
∵1×cos60°=
 ,1×sin60°=
,1×sin60°= ,-1-
,-1- =-
=- ,
,3×cos60°=3×
 =
= ,3×sin60°=3×
,3×sin60°=3×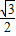 =
=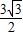 ,3-
,3- =
= ,
,
∴点E、F的坐标分别是E(-
 ,
,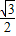 ),F(
),F( ,
, ),
),设公切线EF的解析式是:y=kx+b,
则
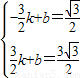 ,
,解得
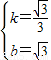 ,
,∴公切线的解析式是y=
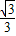 x+
x+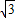 ,
,同理在x轴下方的公切线的解析式是y=-
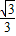 x-
x-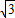 ;
;(3)如图2,EF=AC=
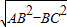 =
=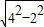 =2
=2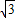 ,
,∴梯形ABFE的面积=
 ×(1+3)×2
×(1+3)×2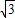 =4
=4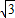 ,
,∵∠BAC=30°,
∴∠EAO=30°+90°=120°,
∴S扇形EAO=
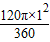 =
=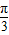 ,S扇形FBO=
,S扇形FBO=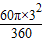 =
=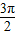 ,
,围成的图形的面积=S梯形ABFE-S扇形EAO-S扇形FBO=4
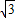 -
-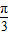 -
-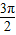 =4
=4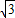 -
-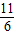 π.
π.故答案为:(1)y=-x2+2x+3,(2)y=-
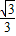 x-
x-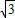 ,(3)4
,(3)4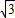 -
- π.
π.点评:本题综合考查了二次函数的问题,根的判别式,二次函数图象与x轴的交点问题,两圆相交的公切线解析式的求解,待定系数法求直线解析式,勾股定理,扇形的面积以及梯形的面积的求解,综合性较强,难度较大,但只要仔细分析也不难解决.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
已知二次函数y=-x2+bx+c的图象过点A(1,2),B(3,2),C(0,-1),D(2,3).点P(x1,y1),Q(x2,y2)也在该函数的图象上,当0<x1<1,2<x2<3时,y1与y2的大小关系正确的是( )
| A、y1≥y2 | B、y1>y2 | C、y1<y2 | D、y1≤y2 |
 (2013•莒南县二模)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
(2013•莒南县二模)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论: 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①ac>0;②a-b+c<0;
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①ac>0;②a-b+c<0;