题目内容
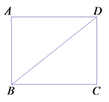
【题目】在四边形ABCD中，有下列条件：①AB
CD；②ADBC；③AC=BD；④AC⊥BD．
（1）从中任选一个作为已知条件，能判定四边形ABCD是平行四边形的概率是 ．
（2）从中任选两个作为已知条件，请用画树状图或列表的方法表示能判定四边形ABCD是矩形的概率，并判断四边形ABCD是菱形的概率？
【答案】（1）
；（2）
，
【解析】（1）根据概率即可得到结论；
（2）列表得出所有等可能的情况数，找出能判定四边形ABCD是矩形和菱形的情况数，即可求出所求的概率．
解：（1）①或②能判定四边形ABCD是平行四边形，
故
故答案为：；
（2）画树状图如图所示，
由树状图得知，从中任选两个作为已知条件共有12结果，能判定四边形ABCD是矩形的有4种，能判定四边形ABCD是菱形的有4种，
∴能判定四边形ABCD是矩形的概率=
=，
能判定四边形ABCD是菱形的概率==，
练习册系列答案
相关题目
【题目】在一次数学实践活动中，观测小组对某品牌节能饮水机进行了观察和记录，当观察到第
分钟时，水温为
，记录的相关数据如下表所示：
第一次加热、降温过程 | … | |||||||||||
t（分钟） | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | … |
y（ | 20 | 40 | 60 | 80 | 100 | 80 | 66.7 | 57.1 | 50 | 44.4 | 40 | … |
（饮水机功能说明：水温加热到
时饮水机停止加热，水温开始下降，当降到
时饮水机又自动开始加热）
请根据上述信息解决下列问题：
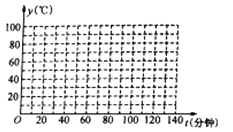
（1）根据表中数据在如给出的坐标系中，描出相应的点；
（2）选择适当的函数，分别求出第一次加热过程和第一次降温过程
关于的函数关系式，并写出相应自变量的取值范围；
（3）已知沏茶的最佳水温是
，若18:00开启饮水机（初始水温
）到当晚20:10，沏茶的最佳水温时间共有多少分钟？
