题目内容
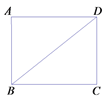
【题目】如图,在矩形ABCD中,对角线BD的长为1,点P是线段BD上的一点,联结CP,将△BCP沿着直线CP翻折,若点B落在边AD上的点E处,且EP//AB,则AB的长等于________.
【答案】![]()
【解析】如下图,设AB= ![]() ,
,
∵四边形ABCD是矩形,
∴AB=CD= ![]() ,AD=BC,∠A=∠ADC=90°,AD∥BC,AB∥CD,
,AD=BC,∠A=∠ADC=90°,AD∥BC,AB∥CD,
∴∠ADB=∠DBC,
∵△PCE是由△PCB沿CP翻折得到的,
∴∠CEP=∠DBC,CE=BC=AD,
∵PE∥AB,AB∥CD,
∴PE∥CD,
∴∠DCE=∠CEP,
∴∠DCE=∠ADB,
∴△CDE∽△DAB,
∴![]() ,即
,即![]() ,
,
又∵BD=1,
∴AD2= ![]() ,
,
∵在Rt△ABD中,AB2+AD2=BD2,
∴![]() ,即
,即![]() ,解得:
,解得: ![]() (舍去),
(舍去),
∴AB=![]() .
.
故答案为: ![]() .
.

练习册系列答案
相关题目
【题目】射击训练班中的甲、乙两名选手在5次射击训练中的成绩依次为(单位:环):
甲:8,8,7,8,9
乙:5,9,7,10,9
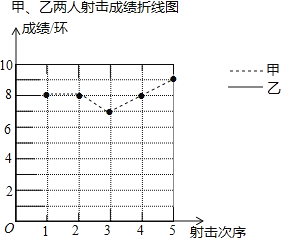
教练根据他们的成绩绘制了如下尚不完整的统计图表:
选手 | 平均数 | 众数 | 中位数 | 方差 |
甲 | 8 | b | 8 | 0.4 |
乙 | α | 9 | c | 3.2 |
根据以上信息,请解答下面的问题:
(1)α= ,b= ,c= ;
(2)完成图中表示乙成绩变化情况的折线;
(3)教练根据这5次成绩,决定选择甲参加射击比赛,教练的理由是什么?
(4)若选手乙再射击第6次,命中的成绩是8环,则选手乙这6次射击成绩的方差与前5次射击成绩的方差相比会 .(填“变大”、“变小”或“不变”)