题目内容
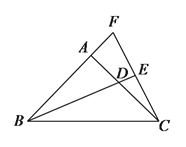
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的平分钱,
的平分钱,![]() 垂足是
垂足是![]() ,
,![]() 和
和![]() 的延长线交于点
的延长线交于点![]() .
.
(![]() )请找出与
)请找出与![]() 相等的所有的角,并证明其中一个.
相等的所有的角,并证明其中一个.
(![]() )求证:
)求证:![]() .
.
【答案】(![]() )
)![]() ,理由见解析;(2)证明见解析.
,理由见解析;(2)证明见解析.
【解析】试题分析:(1)与∠F相等的所有角为∠ADB、∠EDC、∠BCF,选择证明∠F=∠BCF,由已知条件不难证明△FBE≌△CBE,即可证明∠F=∠BCF;(2)先计算出∠ABC和∠ACB的度数,继而求出∠ABD的度数,再由等腰三角形中,已知顶角∠ABC的度数,求出底角∠FCB的度数,接着求出∠ACF的度数,得出∠ABD=∠FCA,再由AB=AC以及∠BAD=∠FAC可得△BAD≌△CAF,所以BD=CF,又因为CE=EF,得证.
试题解析:
(![]() )∠F=∠ADB=∠EDC=∠BCF,
)∠F=∠ADB=∠EDC=∠BCF,
证明∠F=∠BCF,
∵BD平分∠ABC,
∴∠FBE=∠CBE,
∵CE⊥BD于点E,
∴∠FEB=∠CEB=90°,
再△FBE和△CBE中,
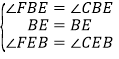 ,
,
∴△FBE≌△CBE(ASA),
∴∠F=∠BCF;
(![]() )∵在Rt△ABC中,∠BAC=90°,AB=AC,
)∵在Rt△ABC中,∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∵BE平分∠ABC,
∴∠ABD=![]() ∠ABC=22.5°,
∠ABC=22.5°,
由(1)可知,∠F=∠FCB=![]() ×(180°-∠ABC)=67.5°,
×(180°-∠ABC)=67.5°,
∴∠FCA=∠FCB-∠ACB=67.5°-45°=22.5°,
∴∠ABD=∠FCA,
在△BAD和△CAF中,
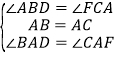 ,
,
∴△BAD≌△CAF(ASA),
∴BD=CF,
∵CE=EF,
∴BD=2EC.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目