题目内容
已知一次函数y=kx+b的图象经过点M(-1,1)及点N(0,2),设该图象与x轴交于点A,与y轴交于点B,问:在x轴上是否存在点P,使ABP为等腰三角形?若存在,把符合条件的点P的坐标都求出来;若不存在,请说明理由.
将点M(-1,1)和点N(0,2)分别代入解析式y=kx+b得,
,
解得
.
则函数解析式为y=x+2.
则函数与y轴的交点B的坐标为(0,2),与x轴的交点坐标为A(-2,0),
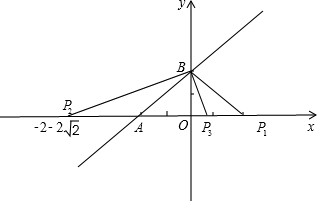
如图:①P1B=AB=2
时,△ABP1为等腰三角形,P1坐标为(2,0);
②P2A=AB=2
时,△ABP2为等腰三角形,P2坐标为(-2-2
,0);
③P3A=AB=2
时,△ABP3为等腰三角形,P3坐标为(2
-2,0);
④当点P于点O重合时,△ABP4为等腰三角形,P4坐标为(0,0).
综上所述,符合条件的点P的坐标为;(2,0),(-2-2
,0),(2
-2,0),(0,0).
|
解得
|
则函数解析式为y=x+2.
则函数与y轴的交点B的坐标为(0,2),与x轴的交点坐标为A(-2,0),
如图:①P1B=AB=2
| 2 |
②P2A=AB=2
| 2 |
| 2 |
③P3A=AB=2
| 2 |
| 2 |
④当点P于点O重合时,△ABP4为等腰三角形,P4坐标为(0,0).
综上所述,符合条件的点P的坐标为;(2,0),(-2-2
| 2 |
| 2 |


练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 y(元)是用水量x(吨)的函数,其函数图象如图所示.
y(元)是用水量x(吨)的函数,其函数图象如图所示.

 之间关系如图.
之间关系如图. km的B处与爷爷相遇,求大刚下山时的速度.
km的B处与爷爷相遇,求大刚下山时的速度.



