题目内容
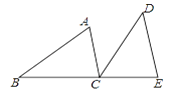
【题目】如图,在Rt△ABC中,∠C=90°,BC=4,AC=8,点D是AC上一个动点,以AB为对角线的所有平行四边形ADBE中,线段DE的最小值是( )

A. 4 B. 2![]() C. 2 D. 6
C. 2 D. 6
【答案】A
【解析】由平行四边形的对角线互相平分、垂线段最短,当OD⊥AC时,DE线段取最小值.
解:∵在Rt△ABC中,∠B=90°,
∴BC⊥AC,
∵四边形ADBE是平行四边形,
∴OD=OE,OA=OB,
∴当OD取最小值时,DE线段最短,此时OD⊥BC.
∴OD∥CB.
又点O是AB的中点,
∴OD是△ABC的中位线,
∴OD=![]() CB=2,
CB=2,
∴ED=2OD=4.
故选A.
“点睛”本题考查了平行四边形的性质,以及垂线段最短.解答该题时,利用了“平行四边形的对角线互相平分”的性质.

练习册系列答案
相关题目