题目内容
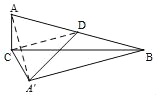
【题目】如图,在△ACB中,∠ACB=90°,∠A=75°,点D是AB的中点.将△ACD沿CD翻折得到△A′CD,连接A′B.

(1)求证:CD∥A′B;
(2)若AB=4,求A′B2的值.
【答案】(1)见解析;(2)12
【解析】
(1)依据直角三角形斜边上中线的性质可知CD=AD,然后依据等腰三角形的性质和三角形的内角和定理可求得∠ADC=30°,由翻折的性质可知∠CDA′=30°,从而可求得∠A′DB的度数,然后依据DA′=DB可求得∠DBA′=30°,从而可证明CD∥A′B;
(2)连结AA′,先证明△ADA′为等边三角形,从而可得到∠AA′D=60°,然后可求得∠AA′B=90°,最后依据勾股定理求解即可.
解:(1)∵∠ACB=90°,点D是AB的中点
∴AD=BD=CD= ![]() AB.
AB.
∴∠ACD=∠A=75°.
∴∠ADC=30°.
∵△A′CD由△ACD沿CD翻折得到,
∴△A′CD≌△ACD.
∴AD=AD,∠A′DC=∠ADC=30°.
∴AD=A′D=DB,∠ADA′=60°.
∴∠A′DB=120°.
∴∠DBA′=∠DA′B=30°.
∴∠ADC=∠DBA'.
∴CD∥A′B.
(2)连接AA′
∵AD=A′D,∠ADA′=60°,
∴△ADA′是等边三角形.
∴AA′=AD= ![]() AB,∠DAA′=60°.
AB,∠DAA′=60°.
∴∠AA′B=180°﹣∠A′AB﹣∠ABA′=90°.
∵AB=4,
∴AA′=2.
∴由勾股定理得:A′B2=AB2﹣AA′2=42﹣22=12.

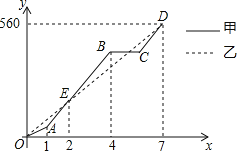
【题目】为了了解学生的课外学习负担,即墨区某中学数学兴趣小组决定对本校学生每天的课外学习情况进行调查,他们随机抽取本校部分学生进行了问卷调查,并将调查结果分为A,B,C,D四个等级,列表如下:
等级 | A | B | C | D |
每天课外学习时间 |
|
|
|
|
根据调查结果绘制了如图所示的两幅不完整的统计图,请你根据图中信息解答下列问题:

![]() 本次抽样调查共抽取了多少名学生?其中学习时间在B等级的学生有多少人?
本次抽样调查共抽取了多少名学生?其中学习时间在B等级的学生有多少人?
![]() 将条形统计图补充完整;
将条形统计图补充完整;
![]() 表示D等级的扇形圆心角的度数是多少?
表示D等级的扇形圆心角的度数是多少?
![]() 该校共有2000名学生,每天课外学习时间在2小时以内的学生有多少人?
该校共有2000名学生,每天课外学习时间在2小时以内的学生有多少人?
【题目】(1)已知![]() ,求代数式
,求代数式![]() 的值.
的值.
(2)2018年6月武侯区某学校开展了主题为“阳光下成长,妙笔绘武侯”学生绘画书法作品比赛,要求参赛学生每人交一件作品. 现将从中挑选的40件参赛作品的成绩(单位:分)统计如下:
等级 | 成绩(用 | 频数 | 频率 |
|
|
| 0.2 |
|
| 20 |
|
|
| 12 | 0.3 |
请根据上表提供的信息,解答下列问题:
①表中![]() 的值为 ,
的值为 ,![]() 的值为 ;
的值为 ;
②将本次获得![]() 等级的参赛作品依次用标签
等级的参赛作品依次用标签![]() 表示. 学校决定从中选取两件作品进行全校展示,
表示. 学校决定从中选取两件作品进行全校展示,![]() 所代表的作品必须参展,另一件作品从
所代表的作品必须参展,另一件作品从![]() 等级余下的作品中抽取,求展示作品刚好是
等级余下的作品中抽取,求展示作品刚好是![]() 的概率.
的概率.