题目内容
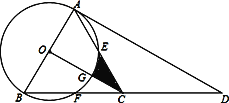
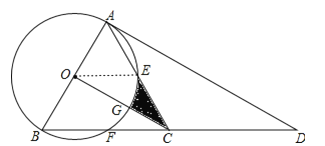
【题目】如图,点D是等边△ABC中BC边的延长线上一点,且AC=CD,以AB为直径作⊙O,分别交边AC、BC于点E、点F.
(1)求证:AD是⊙O的切线;
(2)连接OC,交⊙O于点G,若AB=8,求线段CE、CG与![]() 围成的阴影部分的面积S.
围成的阴影部分的面积S.
【答案】(1)详见解析;(2)![]() .
.
【解析】试题分析:(1)已知△ABC为等边三角形,可得AC=BC,又因AC=CD,所以AC=BC=CD,即可判定△ABD为直角三角形,再根据切线的判定推出结论;(2)连接OE,分别求出△AOE、△AOC,扇形OEG的面积,根据S阴影=S△AOC﹣S等边△AOE﹣S扇形EOG即可求得S.
试题解析:(1)证明:∵△ABC为等边三角形,
∴AC=BC,
又∵AC=CD,
∴AC=BC=CD,
∴△ABD为直角三角形,
∴AB⊥AD,
∵AB为直径,
∴AD是⊙O的切线;
(2)解:连接OE,
∵OA=OE,∠BAC=60°,
∴△OAE是等边三角形,
∴∠AOE=60°,
∵CB=BA,OA=OB,
∴CO⊥AB,
∴∠AOC=90°,
∴∠EOC=30°,
∵△ABC是边长为4的等边三角形,
∴AO=2,由勾股定理得:OC=![]() ,
,
同理等边三角形AOE边AO上高是![]() ,
,
S阴影=S△AOC﹣S等边△AOE﹣S扇形EOG=![]() .
.

练习册系列答案
相关题目