题目内容
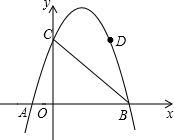
已知抛物线y=ax2+x+c(a≠0)经过A(﹣1,0),B(2,0)两点,与y轴相交于点C,该抛物线的顶点为点M,对称轴与BC相交于点N,与x轴交于点D.
(1)求该抛物线的解析式及点M的坐标;
(2)连接ON,AC,证明:∠NOB=∠ACB;
(3)点E是该抛物线上一动点,且位于第一象限,当点E到直线BC的距离为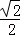 时,求点E的坐标;
时,求点E的坐标;
(4)在满足(3)的条件下,连接EN,并延长EN交y轴于点F,E、F两点关于直线BC对称吗?请说明理由.

(1)求该抛物线的解析式及点M的坐标;
(2)连接ON,AC,证明:∠NOB=∠ACB;
(3)点E是该抛物线上一动点,且位于第一象限,当点E到直线BC的距离为
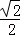 时,求点E的坐标;
时,求点E的坐标;(4)在满足(3)的条件下,连接EN,并延长EN交y轴于点F,E、F两点关于直线BC对称吗?请说明理由.

(1)抛物线为y=﹣x2+x+2=﹣(x﹣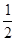 )2+
)2+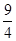 ,顶点M(
,顶点M(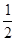 ,
,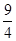 ).
).
证明见解析
(3)E(1,2),
(4)对称;理由见解析
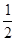 )2+
)2+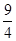 ,顶点M(
,顶点M(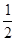 ,
,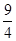 ).
).证明见解析
(3)E(1,2),
(4)对称;理由见解析
试题分析:(1)由待定系数法可求得解析式,然后转化成顶点式即可得顶点坐标.
有两组对应边对应成比例且夹角相等即可知△ABC∽△NBO,由三角形相似的性质即可求得.
作EF⊥BC于F,根据抛物线的解析式先设出E点的坐标,然后根据两直线垂直的性质求得F点的坐标,根据勾股定理即可求得.
(4)延长EF交y轴于Q,根据勾股定理求得FQ的长,再与EF比较即可.
试题解析:(1)∵抛物线y=ax2+x+c(a≠0)经过A(﹣1,0),B(2,0)两点,
∴
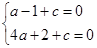 ,
,解得
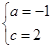 .
.∴抛物线为y=﹣x2+x+2;
∴抛物线为y=﹣x2+x+2=﹣(x﹣
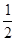 )2+
)2+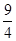 ,
,∴顶点M(
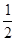 ,
,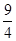 ).
).如图1,

∵A(﹣1,0),B(2,0),C(0,2),
∴直线BC为:y=﹣x+2,
当x=
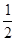 时,y=
时,y=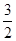 ,
,∴N(
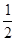 ,
,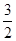 ),
),∴AB=3,BC=2
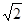 ,OB=2,BN=
,OB=2,BN=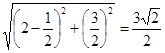 ,
,∴
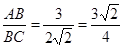 ,
,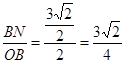 ,
,∵∠ABC=∠NBO,
∴△ABC∽△NBO,
∴∠NOB=∠ACB;
(3)如图2,作EF⊥BC于F,
∵直线BC为y=﹣x+2,
∴设E(m,﹣m2+m+2),直线EF的解析式为y=x+b,
则直线EF为y=x+(﹣m2+2),
解
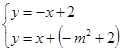 得
得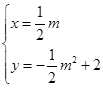 ,
,∴F(
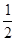 m2,﹣
m2,﹣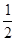 m2+2),
m2+2),∵EF=
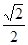 ,
,∴(m﹣
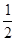 m2)2+(﹣
m2)2+(﹣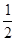 m2+2+m2﹣m﹣2)2=(
m2+2+m2﹣m﹣2)2=(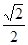 )2,
)2,解得m=1,
∴﹣m2+m+2=2,
∴E(1,2),
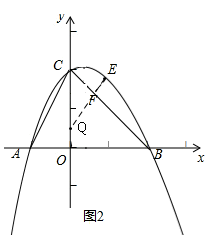
(4)如图2,延长EF交y轴于Q,
∵m=1,
∴直线EF为y=x+1,
∴Q(0,1),
∵F(
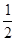 ,
,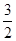 ),
),∴FQ=
 ,
,∵EF=
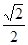 ,EF⊥BC,
,EF⊥BC,∴E、F两点关于直线BC对称.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目


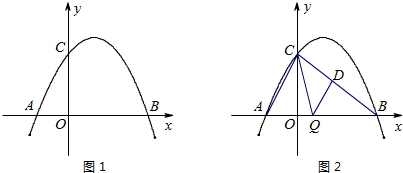

 ;那么x=a-1时,函数值是多少?
;那么x=a-1时,函数值是多少?


 =
= ,当
,当 <
< <
< 时,
时, 
