题目内容
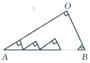
【题目】如图,直角三角板ABC的斜边AB=12cm,∠A=30°,将三角板ABC绕点C顺时针旋转90°至三角板A′B′C′的位置后,再沿CB方向向左平移,使点B′落在原三角板ABC的斜边AB上,则三角板A′B′C′平移的距离为( )
A.6cm
B.(6﹣2![]() )cm
)cm
C.3cm
D.(4![]() ﹣6)cm
﹣6)cm
【答案】B
【解析】解:∵AB=12cm,∠A=30°,
∴BC=![]() AB=
AB=![]() ×12=6cm,
×12=6cm,
由勾股定理得,AC=![]() =
=![]() =6
=6![]() cm,
cm,
∵三角板ABC绕点C顺时针旋转90°得到三角板A′B′C′,
∴B′C′=BC=6cm,
∴AB′=AC﹣B′C′=6![]() ﹣6,
﹣6,
过点B′作B′D⊥AC交AB于D,
则B′D=![]() AB′=
AB′=![]() ×(6
×(6![]() ﹣6)=(6﹣2
﹣6)=(6﹣2![]() )cm.
)cm.
故选B.
【考点精析】本题主要考查了平移的性质的相关知识点,需要掌握①经过平移之后的图形与原来的图形的对应线段平行(或在同一直线上)且相等,对应角相等,图形的形状与大小都没有发生变化;②经过平移后,对应点所连的线段平行(或在同一直线上)且相等才能正确解答此题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目