题目内容
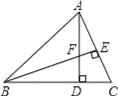
【题目】如图1,把一张长方形的纸片ABCD沿对角线BD折叠,点C落在E处,BE交AD于点F.

(1)求证:FB=FD;
(2)如图2,连接AE,求证:AE∥BD;
(3)如图3,延长BA,DE相交于点G,连接GF并延长交BD于点H,求证:GH垂直平分BD.
【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析.
【解析】
试题(1)根据矩形的性质和折叠的性质可得:AB=DC=DE,∠BAD=∠BCD=∠BED=90°,根据AAS可证△ABF≌△EDF,根据全等三角形的性质可证BF=DF;
(2)根据全等三角形的性质可证:FA=FE,根据等边对等角可得:∠FAE=∠FEA,根据三角形内角和定理可证:2∠AEF +∠AFE =2∠FBD+∠BFD =180°,所以可证∠AEF=∠FBD,根据内错角相等,两直线平行可证AE∥BD;
(3)根据矩形的性质可证:AD=BC=BE,AB=CD=DE,BD=DB,根据SSS可证:△ABD≌△EDB,根据全等三角形的性质可证:∠ABD=∠EDB,根据等角对等边可证:GB=GD,根据HL可证:△AFG≌△EFG,根据全等三角形的性质可证:∠AGF=∠EGF,所以GH垂直平分BD.
试题解析:(1)∵长方形ABCD,
∴AB=DC=DE,∠BAD=∠BCD=∠BED=90°,
在△ABF和△DEF中,
∴△ABF≌△EDF(AAS),
∴BF=DF.
(2)∵△ABF≌△EDF,
∴FA=FE,
∴∠FAE=∠FEA,
又∵∠AFE=∠BFD,且2∠AEF +∠AFE =2∠FBD+∠BFD =180°,
∴∠AEF=∠FBD,
∴AE∥BD,
(3)∵长方形ABCD,
∴AD=BC=BE,AB=CD=DE,BD=DB,
∴△ABD≌△EDB(SSS),
∴∠ABD=∠EDB,
∴GB=GD,
在△AFG和△EFG中,
∠GAF=∠GEF=90°,
FA=FE,
FG=FG,
∴△AFG≌△EFG(HL),
∴∠AGF=∠EGF,
∴GH垂直平分BD.
【方法II】
(1)∵△BCD≌△BED,
∴∠DBC=∠EBD
又∵长方形ABCD,
∴AD∥BC,
∴∠ADB=∠DBC,
∴∠EBD=∠ADB,
∴FB=FD.
(2)∵长方形ABCD,
∴AD=BC=BE,
又∵FB=FD,
∴FA=FE,
∴∠FAE=∠FEA,
又∵∠AFE=∠BFD,且2∠AEF +∠AFE =2∠FBD+∠BFD =180°,
∴∠AEF=∠FBD,
∴AE∥BD,
(3)∵长方形ABCD,
∴AD=BC=BE,AB=CD=DE,BD=DB,
∴△ABD≌△EDB,
∴∠ABD=∠EDB,
∴GB=GD,
又∵FB=FD,
∴GF是BD的垂直平分线,
即GH垂直平分BD.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案