题目内容
【题目】某校教室A位于一地O的正西方向,OA=200米,一部拖拉机从O出发,以5米/秒的速度沿北偏西60°方向行驶,设拖拉机噪音污染半径为125米,试问:教室A是否在噪音污染范围内?若不在,说明理由,若在,求教室A受污染的时间.
【答案】受到污染;30s
【解析】
问教室A是否在拖拉机的噪声污染范围内,其实就是问A到OM的距离是否大于污染半径125m,如果大于则不受影响,反之则受影响.如果过A作AB⊥OM于B,那么AB就是所求的线段.直角三角形AOB中,∠AOB的度数容易求得,又已知了OA的值,那么AB便可求出了.然后进行判断即可.
如果设拖拉机从C到D教室受影响,那么要求教室受影响的时间,其实就是求CD的值,直角三角形ABC中,AB的值已经求得.又有AC的值,那么BC的值就能求出了.CD也就能求出了,然后根据时间=路程÷速度即可得出时间是多少.
解:如图,过点A作AB⊥OM于点B,
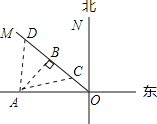
∵∠MON=60°,
∴∠AOM=90°-60°=30°.
在Rt△ABO中,∠ABO=90°,
∵sin∠AOB=![]() ,
,
∴AB=AOsin∠AOB=200×sin30°=100(m).
∵100m<125m.
∴教室A在拖拉机的噪声污染范围内.
根据题意,在OM上取C,D两点,连接AC,AD,使AC=AD=125m,
∵AB⊥OM,
∴B为CD的中点,即BC=DB,
∴BC=![]() =
=![]() =75(m),
=75(m),
∴CD=2BC=150(m).
即影响的时间为![]() =30s.
=30s.

练习册系列答案
相关题目