题目内容
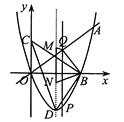
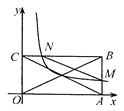
【题目】如图，矩形
的顶点
、
分别在平面直角坐标系的
轴和
轴上，且
，顶点
在第一象限，经过矩形对角线交点的反比例函数
的图像分别与
、
交于点
、
，若
的面积是2，则
的值为________.
【答案】
【解析】
设OC=a，则OA为2a，则B（2a，a），矩形的对角线交点为（a,
a）,由点（a,a）在反比例函数上，知a·a=k，a2=k①；由M、N既在反比例函数上，又在矩形ABCD的边上，可设N（
，a）,M（2a，
），可得BN=2a-，BM=a-,由△NMB得面积为2，
得·（2a-）·（a-）=2②，根据①②即可求出k的值
设OC=a，则OA=2a,
故点B的坐标为（2a，a），矩形的对角线交点为（a,a），
∵反比例函数图像过（a,a），
∴a·a=k，即a2=2k①，
由M、N既在反比例函数上，又在矩形ABCD的边上，
可设N（，a）,M（2a，），
∴BN=2a-，BM=a-,
∵△NMB得面积为2，
∴·（2a-）·（a-）=2 ②；
由①②解得k=.
练习册系列答案
53随堂测系列答案
相关题目
