题目内容
(本小题满分14分)观察下列三个三角恒等式
(1)

(2)

(3)

的特点,由此归纳出一个一般的等式,使得上述三式为它的一个特例,并证明你的结论
(说明:本题依据你得到的等式的深刻性分层评分.)
以下给出两个层次解答供参考.
等式一:若 ,且
,且 ,则
,则
 ................................................ (4分)
................................................ (4分)
证明如下:
因为 ,所以
,所以 ........................................ (6分)
........................................ (6分)
即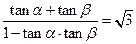 ........................................................... (8分)
........................................................... (8分)
所以 ........................................... (10分)
........................................... (10分)
即
移项得 ......................................... (12分)
......................................... (12分)
等式二:若 ,则
,则
 .................................. (6分)
.................................. (6分)
证明如下:
因为 ................................................. (10分)
................................................. (10分)
所以 ..................................... (12分)
..................................... (12分)
即
移项得 ............................ (14分)解析:
............................ (14分)解析:
略
等式一:若
 ,且
,且 ,则
,则 ................................................ (4分)
................................................ (4分)证明如下:
因为
 ,所以
,所以 ........................................ (6分)
........................................ (6分)即
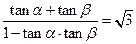 ........................................................... (8分)
........................................................... (8分)所以
 ........................................... (10分)
........................................... (10分)即

移项得
 ......................................... (12分)
......................................... (12分)等式二:若
 ,则
,则 .................................. (6分)
.................................. (6分)证明如下:
因为
 ................................................. (10分)
................................................. (10分)所以
 ..................................... (12分)
..................................... (12分)即

移项得
 ............................ (14分)解析:
............................ (14分)解析:略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图13,二次函数
如图13,二次函数 与y轴交于点C(0,
与y轴交于点C(0, ), 与x轴交于点A、 B,点A的坐标为(2,0).
), 与x轴交于点A、 B,点A的坐标为(2,0).
 与该抛物线交于点Q,与直线BC交于点F,点M 的坐标为(
与该抛物线交于点Q,与直线BC交于点F,点M 的坐标为( ,0).问:是否存在这样的直线
,0).问:是否存在这样的直线 与y轴交于点A,E(0,b)为y轴上一动点,过点E的直线
与y轴交于点A,E(0,b)为y轴上一动点,过点E的直线 与抛物线交于点B、C.
与抛物线交于点B、C.
 与
与 的面积。
的面积。 时,
时, 是以BC为斜边的直角三角形,若存在,求出b;若不存在,说明理由.
是以BC为斜边的直角三角形,若存在,求出b;若不存在,说明理由.