题目内容
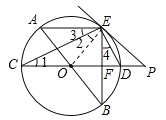
【题目】如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点 F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.
(1)求证:PE是⊙O的切线;
(2)求证:ED平分∠BEP;
(3)若⊙O的半径为5,CF=2EF,求PD的长.

【答案】(1)证明见试题解析;(2)证明见试题解析;(3)![]() .
.
【解析】试题分析:(1)如图,连接OE,证明OE⊥PE即可得出PE是⊙O的切线;
(2)由圆周角定理得到∠AEB=∠CED=90°,进而得到∠3=∠4,结合已知条件证得结论;
(3)设EF=x,则CF=2x,在RT△OEF中,根据勾股定理求出EF的长,进而求得BE,CF的长,在RT△AEB中,根据勾股定理求出AE的长,然后根据△AEB∽△EFP,求出PF的长,即可求得PD的长.
试题解析:(1)如图,连接OE.∵CD是圆O的直径,∴∠CED=90°,∵OC=OE,∴∠1=∠2,又∵∠PED=∠C,即∠PED=∠1,∴∠PED=∠2,∴∠PED+∠OED=∠2+∠OED=90°,即∠OEP=90°,∴OE⊥EP,又∵点E在圆上,∴PE是⊙O的切线;
(2)∵AB、CD为⊙O的直径,∴∠AEB=∠CED=90°,∴∠3=∠4(同角的余角相等),又∵∠PED=∠1,∴∠PED=∠4,即ED平分∠BEP;
(3)设EF=x,则CF=2x,∵⊙O的半径为5,∴OF=2x﹣5,在RT△OEF中, ![]() ,即
,即![]() ,解得x=4,∴EF=4,∴BE=2EF=8,CF=2EF=8,∴DF=CD﹣CF=10﹣8=2,∵AB为⊙O的直径,∴∠AEB=90°,∵AB=10,BE=8,∴AE=6,∵∠BEP=∠A,∠EFP=∠AEB=90°,∴△AEB∽△EFP,∴
,解得x=4,∴EF=4,∴BE=2EF=8,CF=2EF=8,∴DF=CD﹣CF=10﹣8=2,∵AB为⊙O的直径,∴∠AEB=90°,∵AB=10,BE=8,∴AE=6,∵∠BEP=∠A,∠EFP=∠AEB=90°,∴△AEB∽△EFP,∴![]() ,即
,即![]() ,∴PF=
,∴PF=![]() ,∴PD=PF﹣DF=
,∴PD=PF﹣DF=![]() =
=![]() .
.