题目内容
【题目】如图，四边形BFCE是平行四边形，点A、B、C、D在同一条直线上，且AB=CD，连接AE、DF．求证：AE=DF． 
【答案】解：∵四边形BFCE是平行四边形，
∴BE=CF，BE∥CF，
∴∠EBC=∠FCB，
∵点A、B、C、D在同一条直线上，
∴∠ABE=∠DCF，
在△ABE与△DCF中，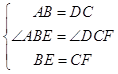 
，
∴△ABE≌△DCF，
∴AE=DF．
【解析】根据四边形BFCE是平行四边形，得到BE=CF，BE∥CF，根据平行线的性质得到∠EBC=∠FCB，根据邻补角的定义得到∠ABE=∠DCF，根据全等三角形的性质即可得到结论．
【考点精析】本题主要考查了平行四边形的性质的相关知识点，需要掌握平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分才能正确解答此题．
练习册系列答案
浙江新课程三维目标测评课时特训系列答案
周周清检测系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
【题目】为了传承优秀传统文化，我市组织了一次初三年级1 200名学生参加的“汉字听写”大赛，为了更好地了解本次大赛的成绩分布情况，随机抽取了100名学生的成绩(满分50分)，整理得到如下的统计图表：
成绩(分) | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
人数 | 1 | 2 | 3 | 3 | 6 | 7 | 5 | 8 | 15 | 9 | 11 | 12 | 8 | 6 | 4 |
成绩分组 | 频数 | 频率(百分比) |
35≤x<38 | 3 | 0.03 |
38≤x<41 | a | 0.12 |
41≤x<44 | 20 | 0.20 |
44≤x<47 | 35 | 0.35 |
47≤x≤50 | 30 | b |
请根据所提供的信息解答下列问题：
(1)频率统计表中a＝________，b＝_______；
(2)请补全频数分布直方图；
(3)请根据抽样统计结果，估计该次大赛中成绩不低于41分的学生有多少人？
