题目内容
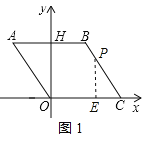
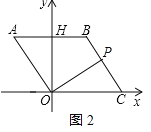
【题目】如图，在平面直角坐标系中，点O是坐标原点，四边形ABCO是菱形，点C在x轴的正半轴上，AB边交y轴于点H，OC＝4，∠BCO＝60°．
（1）求点A的坐标
（2）动点P从点A出发，沿折线A﹣B一C的方向以2个单位长度秒的速度向终点C匀速运动，设△POC的面积为S，点P的运动时间为t秒，求S与t之间的函数关系式（要求写出自变量t的取值范围）；
（3）在（2）的条件下，直接写出当t为何值时△POC为直角三角形．
【答案】（1）
；（2）
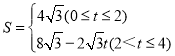；（3）t=1或t=3
【解析】
（1）首先做辅助线BF⊥OC于F，AG⊥x轴于G，在Rt△BCF中，求出BF，BF=AG，OG=CF，又因为A在第二象限，即可得出点A的坐标.
（2）需分两种情况：
①当
时，即P从A运动到B，求出三角形的面积，
②当
时，即P从B运动到C，求出三角形的面积，
将两种情况综合起来即可得出最后结果.
（3）在（2）的条件下，当t=1或t=3时，根据三角形的性质，可以判定△POC为直角三角形．
（1）如图，做辅助线BF⊥OC于F，AG⊥x轴于G
在Rt△BCF中，∠BCF=60°，BC=4，CF=2，BF=
，
BF=AG=，OG=CF=2，A在第二象限，
故点A的坐标为（-2，）
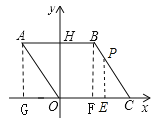
（2）当时，即P从A运动到B，S=
=
，
设P（m，n），∠BCO＝60°，
当时，即P从B运动到C，BP=2t，
则cos30°=
=
,
,
则S=
=
综上所述，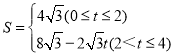
（3）在（2）的条件下，当t=1或t=3时，△POC为直角三角形．
【题目】山地自行车越来越受到中学生的喜爱，各种品牌相继投放市场，某车行经营的A型车去年销售总额为5万元，今年每辆销售价比去年降低400元，若卖出的数量相同，销售总额将比去年减少20%．
（1）今年A型车每辆售价多少元？（用列方程的方法解答）
（2）该车行计划新进一批A型车和新款B型车共60辆，且B型车的进货数量不超过A型车数量的两倍，应如何进货才能使这批车获利最多？
A，B两种型号车的进货和销售价格如下表：
A型车 | B型车 | |
进货价格（元） | 1100 | 1400 |
销售价格（元） | 今年的销售价格 | 2000 |
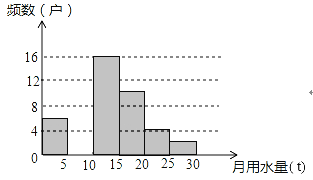
【题目】八年级（1）班同学为了解某小区家庭月均用水情况，随机调査了该小区部分家庭，并将调查数据整理成如下两幅不完整的统计图表：
月均用水量x（t） | 频数（户） | 频率 |
0＜x≤5 | 6 | 0.12 |
5＜x≤10 | m | 0.24 |
10＜x≤15 | 16 | 0.32 |
15＜x≤20 | 10 | 0.20 |
20＜x≤25 | 4 | n |
25＜x≤30 | 2 | 0.04 |
请根据以上信息，解答以下问题：
（1）直接写出频数分布表中的m、n的值并把频数直方图补充完整；
（2）求出该班调查的家庭总户数是多少？
（3）求该小区用水量不超过15的家庭的频率．
