题目内容
【题目】等腰三角形一腰上的高与另一边的夹角为80°，则顶角的度数为_______．
【答案】160°或10°或170°
【解析】
等腰三角形一腰上的高与底边的夹角为80°，根据直角三角形两锐角互余求出底角的度数，再根据等腰三角形两底角相等列式进行计算即可得解；
等腰三角形一腰上的高与另一腰的夹角为80°，首先根据题意画出图形，一种情况等腰三角形为锐角三角形，即可推出顶角的度数为10°；另一种情况等腰三角形为钝角三角形，由题意，即可推出顶角的度数为170°．
解：如图，AB=AC，
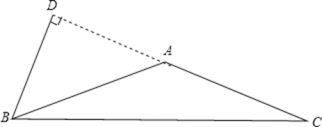
∵一腰上的高与底边的夹角为∠DBC=80°，
∴底角∠C=90°-80°=10°，
∴顶角∠BAC=180°-2×10°=180°-20°=160°．
故答案为：160°；
如图，等腰三角形为锐角三角形，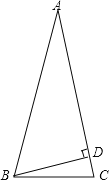
∵BD⊥AC，∠ABD=80°，
∴∠A=10°，
即顶角的度数为10°；
如图，等腰三角形为钝角三角形，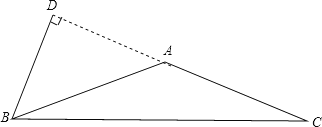
∵BD⊥AC，∠DBA=80°，
∴∠BAD=10°，
∴∠BAC=170°．
故答案为：160°或10°或170°．
练习册系列答案
阅读快车系列答案
相关题目
