ĢāÄæÄŚČŻ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ![]() ÖŠ£¬
ÖŠ£¬![]() £¬
£¬![]() ÓŚµć
ÓŚµć![]() £¬
£¬![]() £¬
£¬![]() .µć
.µć![]() “Óµć
“Óµć![]() ³ö·¢£¬ŌŚĻ߶Ī
³ö·¢£¬ŌŚĻ߶Ī![]() ÉĻŅŌĆæĆė
ÉĻŅŌĆæĆė![]() µÄĖŁ¶ČĻņµć
µÄĖŁ¶ČĻņµć![]() ŌČĖŁŌĖ¶Æ£»Óė“ĖĶ¬Ź±£¬“¹Ö±ÓŚ
ŌČĖŁŌĖ¶Æ£»Óė“ĖĶ¬Ź±£¬“¹Ö±ÓŚ![]() µÄÖ±Ļß
µÄÖ±Ļß![]() “Óµ×±ß
“Óµ×±ß![]() ³ö·¢£¬ŅŌĆæĆė
³ö·¢£¬ŅŌĆæĆė![]() µÄĖŁ¶ČŃŲ
µÄĖŁ¶ČŃŲ![]() ·½ĻņŌČĖŁĘ½ŅĘ£¬·Ö±š½»
·½ĻņŌČĖŁĘ½ŅĘ£¬·Ö±š½»![]() ”¢
Ӣ![]() Ӣ
”¢![]() ÓŚµć
ÓŚµć![]() ”¢
Ӣ![]() Ӣ
”¢![]() £¬µ±µć
£¬µ±µć![]() µ½“ļµć
µ½“ļµć![]() Ź±£¬µć
Ź±£¬µć![]() ÓėÖ±Ļß
ÓėÖ±Ļß![]() Ķ¬Ź±Ķ£Ö¹ŌĖ¶Æ£¬ÉčŌĖ¶ÆŹ±¼äĪŖ
Ķ¬Ź±Ķ£Ö¹ŌĖ¶Æ£¬ÉčŌĖ¶ÆŹ±¼äĪŖ![]() Ćė£Ø
Ćė£Ø![]() £©.
£©.
£Ø1£©µ±![]() Ź±£¬Į¬½Ó
Ź±£¬Į¬½Ó![]() ”¢
”¢![]() £¬ĒóÖ¤£ŗĖıߊĪ
£¬ĒóÖ¤£ŗĖıߊĪ![]() ĪŖĮāŠĪ£»
ĪŖĮāŠĪ£»
£Ø2£©µ±![]() Ź±£¬Ēó
Ź±£¬Ēó![]() µÄĆ껿£»
µÄĆ껿£»
£Ø3£©ŹĒ·ń“ęŌŚÄ³Ņ»Ź±æĢ![]() £¬Ź¹
£¬Ź¹![]() ĪŖŅŌµć
ĪŖŅŌµć![]() »ņ
»ņ![]() ĪŖÖ±½Ē¶„µćµÄÖ±½ĒČż½ĒŠĪ£æČō“ęŌŚ£¬ĒėĒó³ö“ĖŹ±æĢ
ĪŖÖ±½Ē¶„µćµÄÖ±½ĒČż½ĒŠĪ£æČō“ęŌŚ£¬ĒėĒó³ö“ĖŹ±æĢ![]() µÄÖµ£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ.
µÄÖµ£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ.
”¾“š°ø”æ£Ø1£©¼ū½āĪö£»£Ø2£©![]() £»£Ø3£©“ęŌŚŅŌµć
£»£Ø3£©“ęŌŚŅŌµć![]() ĪŖÖ±½Ē¶„µćµÄÖ±½ĒČż½ĒŠĪ.“ĖŹ±£¬
ĪŖÖ±½Ē¶„µćµÄÖ±½ĒČż½ĒŠĪ.“ĖŹ±£¬![]() .
.
”¾½āĪö”æ
£Ø1£©øł¾ŻĮāŠĪµÄÅŠ¶Ø¶ØĄķ¼“æÉĒó½ā£»
£Ø2£©ÓÉ£Ø1£©ÖŖ![]() £¬¹Ź
£¬¹Ź![]() £¬¹Ź
£¬¹Ź ![]() £¬æÉĒóµĆ
£¬æÉĒóµĆ![]() £¬
£¬
![]() £¬ ŌŁøł¾ŻČż½ĒŠĪµÄĆ껿¹«Ź½¼“æÉĒó½ā£»
£¬ ŌŁøł¾ŻČż½ĒŠĪµÄĆ껿¹«Ź½¼“æÉĒó½ā£»
£Ø3£©øł¾ŻĢāŅā·Ö¢ŁČōµć![]() ĪŖÖ±½Ē¶„µć£¬ ¢ŚČōµć
ĪŖÖ±½Ē¶„µć£¬ ¢ŚČōµć![]() ĪŖÖ±½Ē¶„µć£¬ øł¾ŻĻąĖĘČż½ĒŠĪµÄŠŌÖŹ¼“æÉĒó½ā.
ĪŖÖ±½Ē¶„µć£¬ øł¾ŻĻąĖĘČż½ĒŠĪµÄŠŌÖŹ¼“æÉĒó½ā.
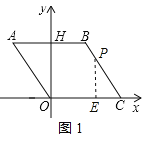
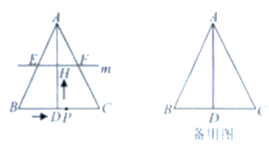
£Ø1£©Ö¤Ć÷£ŗČēĶ¼1£¬µ±![]() Ź±£¬
Ź±£¬![]() £¬
£¬
Ōņ![]() ĪŖ
ĪŖ![]() µÄÖŠµć£¬ÓÖ”ß
µÄÖŠµć£¬ÓÖ”ß![]() £¬
£¬
”ą![]() ĪŖ
ĪŖ![]() µÄ“¹Ö±Ę½·ÖĻߣ¬”ą
µÄ“¹Ö±Ę½·ÖĻߣ¬”ą![]() £¬
£¬![]() .
.
”ß![]() £¬”ą
£¬”ą![]() .
.
”ß![]() £¬”ą
£¬”ą![]() £¬
£¬![]() £¬
£¬
”ą![]() £¬”ą
£¬”ą![]() £¬
£¬
”ą![]() £¬¼“ĖıߊĪ
£¬¼“ĖıߊĪ![]() ĪŖĮāŠĪ.
ĪŖĮāŠĪ.
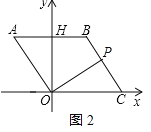
£Ø2£©ČēĶ¼2£¬ÓÉ£Ø1£©ÖŖ![]() £¬
£¬
”ą![]() £¬
£¬
”ą![]() £¬¼“
£¬¼“![]() £¬½āµĆ£ŗ
£¬½āµĆ£ŗ![]() £¬
£¬
![]() £¬
£¬
![]() £»
£»
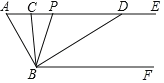
£Ø3£©¢ŁČōµć![]() ĪŖÖ±½Ē¶„µć£¬ČēĶ¼3¢Ł£¬
ĪŖÖ±½Ē¶„µć£¬ČēĶ¼3¢Ł£¬
“ĖŹ±![]() £¬
£¬![]() £¬
£¬![]() .
.
”ß![]() £¬”ą
£¬”ą![]() £¬
£¬
¼“£ŗ![]() £¬“Ė±ČĄżŹ½²»³ÉĮ¢£¬¹Ź²»“ęŌŚŅŌµć
£¬“Ė±ČĄżŹ½²»³ÉĮ¢£¬¹Ź²»“ęŌŚŅŌµć![]() ĪŖÖ±½Ē¶„µćµÄÖ±½ĒČż½ĒŠĪ£»
ĪŖÖ±½Ē¶„µćµÄÖ±½ĒČż½ĒŠĪ£»
¢ŚČōµć![]() ĪŖÖ±½Ē¶„µć£¬ČēĶ¼3¢Ś£¬
ĪŖÖ±½Ē¶„µć£¬ČēĶ¼3¢Ś£¬
“ĖŹ±![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() .
.
”ß![]() £¬”ą
£¬”ą![]() £¬¼“£ŗ
£¬¼“£ŗ![]() £¬
£¬
½āµĆ![]() .¹Ź“ęŌŚŅŌµć
.¹Ź“ęŌŚŅŌµć![]() ĪŖÖ±½Ē¶„µćµÄÖ±½ĒČż½ĒŠĪ.“ĖŹ±£¬
ĪŖÖ±½Ē¶„µćµÄÖ±½ĒČż½ĒŠĪ.“ĖŹ±£¬![]() .
.

”¾ĢāÄæ”æijČü¼¾ĄŗĒņ¼×A ĮŖČü²æ·ÖĒņ¶Ó»ż·Ö°ńČēĻĀ£ŗ
¶ÓĆū | ±ČČü³”“Ī | Ź¤³” | øŗ³” | »ż·Ö |
°ĖŅ»Ė«Ā¹ | 20 | 18 | 2 | 38 |
±±¾©Ź×øÖ | 20 | 14 | 6 | 34 |
Õć½ĶņĀķ | 20 | 7 | 13 | 27 |
Éņ²æŠŪŹØ | 20 | 0 | 20 | 20 |
£Ø1£©øƱČČüŹ¤1³”µÄ»ż·ÖĪŖ ·Ö£¬øŗ1³”µÄ»ż·ÖĪŖ ·Ö£¬ ĮŠŹ½±ķŹ¾»ż·ÖÓėŹ¤”¢øŗ³”ŹżÖ®¼äµÄŹżĮæ¹ŲĻµ£¬¼ŁÉ菤³”ŹżĪŖm³”£¬ŌņÕā“Ī±ČČüµÄ»ż·ÖŹĒ £ØÖ±½ÓŠ“³ö½į¹ū£©
£Ø2£©Ä³¶ÓµÄŹ¤³”×Ü»ż·ÖÄܵČÓŚĖüµÄøŗ³”×Ü»ż·ÖĀš£æ