题目内容
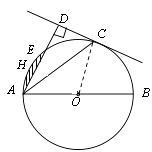
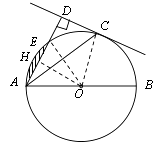
【题目】如图,AB为⊙O的直径,点C为圆上一点,AD和过点C的切线互相垂直,垂足为点D,AD交⊙O于点E.
(1)求证:AC平分∠BAD;
(2)若CD=3,AC=6,求图中阴影部分面积.
【答案】
(1)解:连结OC,
∵OA=OC,
∴∠OAC=∠OCA.
∵CD是⊙O的切线,
∴OC⊥CD,
∵AD⊥CD,
∴OC∥AD.
∴∠OCA=∠CAD,
∴∠CAD=∠CAO.
∴AC平分∠BAD.
(2)解:连结OE,作OH⊥AE,
∵CD=3,AC=6,AD⊥CD,
∴∠CAD=∠CAO =∠OCA=30°,
∴∠DAO=60°,∠AOC=120°.
∵OE=OA,
∴△AOE为等边三角形.
∴∠AOE=60°,
∴OE⊥CA.
∴AO=OC=2 ![]() ,OH=3.
,OH=3.
∴S阴影= S扇形-S△AOE= ![]() -3
-3 ![]() =2π-3
=2π-3 ![]()
【解析】(1)连结OC,根据等边对等角得出∠OAC=∠OCA,根据切线的性质得出OC⊥CD,又AD⊥CD,根据同一平面内垂直于同一直线的两条直线互相平行得出OC∥AD,根据二直线平行内错角相等得出∠OCA=∠CAD,进而得出结论;
(2)连结OE,作OH⊥AE,根据Rt△ADC中一条直角边等于斜边的一半从而这条直角边所对的锐角等于30![]() ,得出∠CAD=∠CAO =∠OCA=30°,进而得出∠DAO=60°,∠AOC=120°,根据含60
,得出∠CAD=∠CAO =∠OCA=30°,进而得出∠DAO=60°,∠AOC=120°,根据含60![]() 的等腰三角形是等边三角形得出△AOE为等边三角形,根据等边三角形的性质得出∠AOE=60°,进而得出OE⊥CA,根据含30
的等腰三角形是等边三角形得出△AOE为等边三角形,根据等边三角形的性质得出∠AOE=60°,进而得出OE⊥CA,根据含30![]() 的直角三角形的边角关系得出AO=OC=2
的直角三角形的边角关系得出AO=OC=2 ![]() ,OH=3,然后利用S阴影= S扇形-S△AOE算出结果。
,OH=3,然后利用S阴影= S扇形-S△AOE算出结果。
【考点精析】关于本题考查的平行线的判定与性质和三角形的面积,需要了解由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质;三角形的面积=1/2×底×高才能得出正确答案.

 名校课堂系列答案
名校课堂系列答案