��Ŀ����
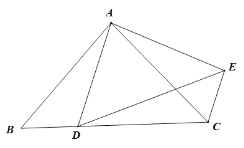
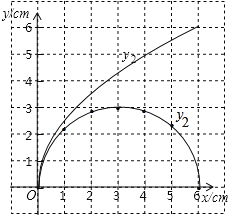
����Ŀ������ͼ��ʾ�İ�Բ�У�P��ֱ��AB��һ���㣬����P��PC��AB�ڵ�P������Բ�ڵ�C������AC����֪AB=6cm����A��P�����ľ���Ϊxcm��P��C�����ľ���Ϊy1cm��A��C�����ľ���Ϊy2cm��
С�ϸ���ѧϰ�����ľ��飬�ֱ�Ժ���y1��y2���Ա���x�ı仯���仯�Ĺ��ɽ�����̽����
������С�ϵ�̽�����̣��벹��������
��1�������±����Ա���x��ֵ����ȡ�㡢��ͼ���������ֱ�õ���y1��y2��x�ļ����Ӧֵ��
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 0 | 2.24 | 2.83 | 2.83 | 2.24 | 0 | |
y2/cm | 0 | 2.45 | 3.46 | 4.24 | 4.90 | 5.48 | 6 |
��2����ͬһƽ��ֱ������ϵxOy�У������ȫ��ı��и�����ֵ����Ӧ�ĵ㣨x��y1������x��y2��������������y1��y2��ͼ��
��3����Ϻ���ͼ������⣺����APC��һ������30��ʱ��AP�ij���ԼΪ cm��
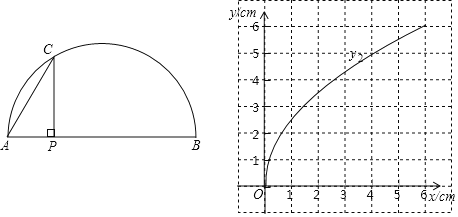
���𰸡�(1)3;��2����ͼ����������3��4.5.
��������
��1����ΪPC=3ʱ��PA=PB=3���Ƴ�PC�ǡ�O�İ뾶���ɽ�����⣻
��2��������㷨��������ͼ�ɣ�
��3���������ν�ϵ�˼�������⼴��.
��1����ΪPC=3ʱ��PA=PB=3��
��PC�ǡ�O�İ뾶��
��PC=3cm����x=3ʱ��y1=3��
��2��������㷨��������ͼ�ɣ�
��3�����ͼ���֪������ACP=30��ʱ��AP=![]() AC=
AC=![]() ��
��![]() AB=1.50cm��
AB=1.50cm��
���ݶԳ��ԣ����ͼ���֪������CAP=30��ʱ��PB=1.50cm��PA=4.50cm��

����Ŀ�����ٹ�·ij�շ�վ���Ƿ����б��Ϊ![]() �����С�ͳ��շѳ��ڣ��ٶ����շѳ���ÿ20����ͨ��С�ͳ��������ֱ��Dz����.ͬʱ�������е�ij�����շѳ��ڣ�����������20����һ��ͨ����С�ͳ�������¼���£�
�����С�ͳ��շѳ��ڣ��ٶ����շѳ���ÿ20����ͨ��С�ͳ��������ֱ��Dz����.ͬʱ�������е�ij�����շѳ��ڣ�����������20����һ��ͨ����С�ͳ�������¼���£�
�շѳ��ڱ�� |
|
|
|
|
|
ͨ��С�ͳ����������� | 260 | 330 | 300 | 360 | 240 |
��![]() ����շѳ����У�ÿ20����ͨ��С�ͳ���������һ�����ڵı����___________.
����շѳ����У�ÿ20����ͨ��С�ͳ���������һ�����ڵı����___________.