Question

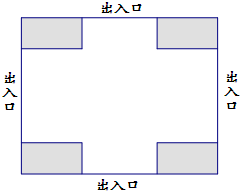
如图，把一张长12cm，宽10cm的矩形硬纸板的四周各剪去一个同样大小的正方形，再折合成一个无盖的长方体盒子（纸板的厚度忽略不计）．
（1）要使长方体盒子的底面积为48cm²，那么剪去的正方形的边长为多少？
（2）你感到折合而成的长方体盒子的侧面积会不会有更大的情况？如果有，请你求出最大值和此时剪去的正方形的边长；如果没有，请你说明理由．

Answer 1

（1）设剪去的正方形的边长为xcm，
则（12-2x）（10-2x）=48，
解之得x₁=2，x₂=9（不合题意，舍去），
故x=2cm．

（2）设侧面积为y，
则y=2（12-2x）x+2（10-2x）x
=-8x²+44x
=-8（x-

11

4

）²+

121

2

，
由以上函数图象知，
故在正方形的边长为

11

4

cm时，长方体盒子的侧面积最大，最大面积为

121

2

cm²