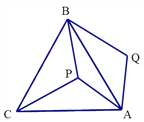
题目内容
【题目】如图, ![]() 是等边三角形
是等边三角形![]() 内一点,将线段
内一点,将线段![]() 绕点
绕点![]() 顺时针旋转60°得到线段
顺时针旋转60°得到线段![]() ,连接
,连接![]() .若
.若![]() ,则四边形
,则四边形![]() 的面积为____.
的面积为____.
【答案】24+9![]() .
.
【解析】试题分析:如图,连结PQ,根据等边三角形的性质得∠BAC=60°,AB=AC,再根据旋转的性质得AP=PQ=6,∠PAQ=60°,即可判定△APQ为等边三角形,所以PQ=AP=6;在△APC和△ABQ中,AB=AC,∠CAP=∠BAQ,AP=PQ,利用SAS判定△APC≌△ABQ,根据全等三角形的性质可得PC=QB=10;在△BPQ中,已知PB2=82=64,PQ2=62,BQ2=102,即PB2+PQ2=BQ2,所以△PBQ为直角三角形,∠BPQ=90°,所以S四边形APBQ=S△BPQ+S△APQ=![]() ×6×8
×6×8![]() +×62=24+9
+×62=24+9![]() .
.


练习册系列答案
相关题目