题目内容
【题目】已知：如图，在正方形ABCD中，M，N分别是边AD，CD上的点，且∠MBN=45°，连接MN。
求证：MN＝AM+CN.
【答案】证明见解析
【解析】先构造全等三角形，用得到的结论判断出△MBN≌△EBN，得出MN=EN，即可.
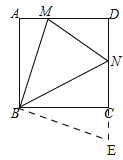
证明: 延长DC到E使CE=AM，连结BE
∵正方形ABCD，∴AB= BC，∠A=∠ABC=∠BCD=90。
∴∠BCE=∠A=90。∴△ABM≌△CBE，∴∠1=∠2，BM=BE，
∵∠MBN=45。∴∠1+∠3=45。∴∠2+∠3=45。
即∠EBN=∠MBN
∴△MBN≌△EBN，
∴MN=EN，∴MN=AM+CN.
“点睛”此题考查了正方形的性质，全等三角形的性质和判定，构造全等三角形是解答此题的关键.
练习册系列答案
相关题目
