题目内容
(1)图1是由若干个小圆圈堆成的一个形如等边三角形的图案,最上面一层有一个圆圈,以下各层均比上一层多一个圆圈,一共堆了n层.将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为:1+2+3+…+n=
(2)小明在一次数学活动中,为了求
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 24 |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 24 |
| 1 |
| 2n |
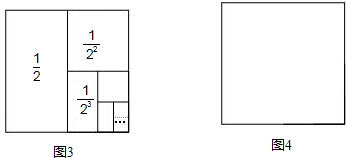
(3)请你利用图4,再设计一个能求
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 24 |
| 1 |
| 2n |
分析:(1)图2中圆点的个数是图1中圆点个数的2倍,图2总圆点个数为n×(n+1),所以图1中圆点是个数为:
(2)设正方形的面积为1,每次划分都是将原图形化成两个面积相等的图象,当化到第n个时,所剩的最小图形的面积是
,所以
+
+
+
+…+
表示的面积等于1-
.
(3)在划分图形时每次划分都是上一级图形面积的一半.
| n(n+1) |
| 2 |
(2)设正方形的面积为1,每次划分都是将原图形化成两个面积相等的图象,当化到第n个时,所剩的最小图形的面积是
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 24 |
| 1 |
| 2n |
| 1 |
| 2n |
(3)在划分图形时每次划分都是上一级图形面积的一半.
解答: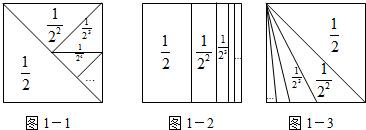 解:由分析得:(1)1+2+3+…+n=
解:由分析得:(1)1+2+3+…+n=
;
(2)
+
+
+
+…+
=1-
.
(3)如图1-1或如图1-2或如图1-3等.
 解:由分析得:(1)1+2+3+…+n=
解:由分析得:(1)1+2+3+…+n=| n(n+1) |
| 2 |
(2)
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 24 |
| 1 |
| 2n |
| 1 |
| 2n |
(3)如图1-1或如图1-2或如图1-3等.
点评:本题解答关键是利用图形的面积表示所求表达式的值,在图形划分时每一次划分都是上一级图形面积的一半.

练习册系列答案
相关题目
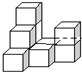 18、如图,是由若干个完全相同的小正方体组成的一个几何体.
18、如图,是由若干个完全相同的小正方体组成的一个几何体.

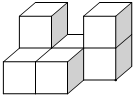 如图,是由若干个大小相同且边长为1的小正方体堆砌而成的几何体,那么其三种视图的面积之和是( )
如图,是由若干个大小相同且边长为1的小正方体堆砌而成的几何体,那么其三种视图的面积之和是( )
 2008年奥运期间,小区物业用花盆妆点院落.下列的每一个图都是由若干个花盆组成的正方形图案.
2008年奥运期间,小区物业用花盆妆点院落.下列的每一个图都是由若干个花盆组成的正方形图案.