题目内容
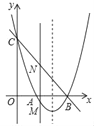
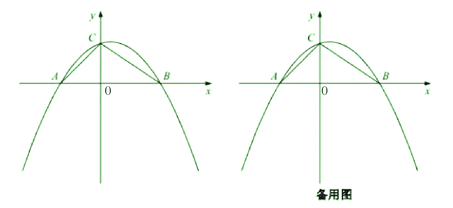
【题目】如图,抛物线![]() (其中m>0)与x轴交于A、B两点(A在B的左侧),与y轴交于点C,连接AC、BC
(其中m>0)与x轴交于A、B两点(A在B的左侧),与y轴交于点C,连接AC、BC
(1)直接写出点A、点C的坐标;
(2)当∠ACB=90°时,点D是第一象限抛物线上一动点,连接OD,当OD的长最小时,求点D的坐标;
(3)直线![]() 经过点B,与抛物线交于另一点G,点P在y轴上,点Q在抛物线上,以点B、G、P、Q为顶点的四边形能否为矩形?若能,求出点P的坐标,若不能,请说明理由.
经过点B,与抛物线交于另一点G,点P在y轴上,点Q在抛物线上,以点B、G、P、Q为顶点的四边形能否为矩形?若能,求出点P的坐标,若不能,请说明理由.
(4) 当tan∠CBO=![]() 时,动点P从点A出发,以每秒2个单位长度的速度沿射线AO方向匀速运动,动点Q从点B出发,以每秒1个单位长度的速度沿射线BO方向匀速运动,P、Q两点同时运动,相遇时停止,在运动过程中,以PQ为一边在x轴上方作正方形PQMN,设运动时间为t秒.不妨设正方形PQMN和△ABC重叠部分的面积为S,请直接写出S关于t的函数表达式.
时,动点P从点A出发,以每秒2个单位长度的速度沿射线AO方向匀速运动,动点Q从点B出发,以每秒1个单位长度的速度沿射线BO方向匀速运动,P、Q两点同时运动,相遇时停止,在运动过程中,以PQ为一边在x轴上方作正方形PQMN,设运动时间为t秒.不妨设正方形PQMN和△ABC重叠部分的面积为S,请直接写出S关于t的函数表达式.
【答案】(1)A点坐标为(-2,0),C点坐标为(0,2)(2)D点坐标为(![]() ,
,![]() )(3)P点为(2,-
)(3)P点为(2,-![]() m-9)(4)当PQ≥OC时S=-
m-9)(4)当PQ≥OC时S=-![]() 2+6,当PQ<OC时S=9t2-36t+36
2+6,当PQ<OC时S=9t2-36t+36
【解析】
(1)C点纵坐标为当x=0时,y的值,A点横坐标为当y=0时,x的值.
(2)先根据题意求出抛物线解析式,再设D点坐标由两点距离公式即可得到.
(3)先求出 G点坐标,在得到GP解析式,即可求得P点坐标.
(4)先求得m的值,再分情况讨论当PQ≥OC时与PQ<OC时S的值.
(1)∵抛物线![]() (其中m>0)与x轴交于A、B两点,与y轴交于点C
(其中m>0)与x轴交于A、B两点,与y轴交于点C
∴A点坐标为(-2,0),C点坐标为(0,2)
(2)当∠ACB=90°时,B点坐标为(2,0)此时抛物线为y=-![]() (x+2)(x-2)=-
(x+2)(x-2)=-![]() x2+2
x2+2
设D点坐标为(x,-![]() x2+2)
x2+2)
则OD=![]()
∴当x2=![]() 时,即x=
时,即x=![]() 时OD最小.(x=-
时OD最小.(x=-![]() 舍去)
舍去)
此时D点坐标为(![]() ,
,![]() )
)
(3)![]() 经过点B(m,0)
经过点B(m,0)
∴b=-![]() m, 即y=
m, 即y=![]() x-
x-![]() m
m
∵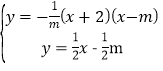
∴x=-![]() m-2
m-2
∴G点为(-![]() m-2,-
m-2,-![]() m-1)
m-1)
∵直线![]() 与直线GP垂直
与直线GP垂直
∴GP的解析式为y=-2x+b2
G点带入得b2=-![]() m-5
m-5
∴GP的解析式为y=-2x-![]() m-5
m-5
∵P点在对称轴x=2上
∴y=-2×2-![]() m-5
m-5
∴P点为(2,-![]() m-9)
m-9)
(4) 当tan∠CBO=![]() 时,
时,![]() ,即BO=4
,即BO=4
∴m=4
∴抛物线解析式为![]()
设AP=2t,BQ=t,PQ=6-3t
当PQ≥OC时,即6-3t≥2
t≤![]()
设PN与AC交于G点,MQ与BC交于H
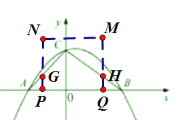
S=S△ABC-S△AGP-S△BHQ=![]() ×6×2-
×6×2-![]() ×4t2-
×4t2-![]() t·
t·![]() t=-
t=-![]() 2+6
2+6
当PQ<OC时,即6-3t<2
即t>![]()
S=SPQMN=(6-3t)2=9t2-36t+36.
综上,当PQ≥OC时S=-![]() 2+6,当PQ<OC时S=9t2-36t+36.
2+6,当PQ<OC时S=9t2-36t+36.

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案【题目】在数学活动课上,老师提出了一个问题:把一副三角尺如图摆放,直角三角尺的两条直角边分别垂直或平行,60°角的顶点在另一个三角尺的斜边上移动,在这个运动过程中,有哪些变量,能研究它们之间的关系吗?
小林选择了其中一对变量,根据学习函数的经验,对它们之间的关系进行了探究.
下面是小林的探究过程,请补充完整:
(1)画出几何图形,明确条件和探究对象;
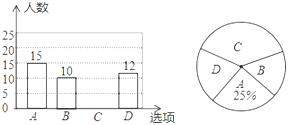
如图2,在Rt△ABC中,∠C=90°,AC=BC=6cm,D是线段AB上一动点,射线DE⊥BC于点E,∠EDF=60°,射线DF与射线AC交于点F.设B,E两点间的距离为xcm,E,F两点间的距离为ycm.
(2)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 6.9 | 5.3 | 4.0 | 3.3 | 4.5 | 6 |
(说明:补全表格时相关数据保留一位小数)
(3)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(4)结合画出的函数图象,解决问题:当△DEF为等边三角形时,BE的长度约为 cm.