题目内容
已知t为一元二次方程x2-3x+1=0的根.
(1)对任一给定的有理数a,求有理数b,c,使得(t+a)(bt+c)=1成立;
(2)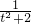 表示成dt+e的形式,其中d,e为有理数.
表示成dt+e的形式,其中d,e为有理数.
解:(1)解方程x2-3x+1=0得t= 是无理数,
是无理数,
由(t+a)(bt+c)=1得bt2+(ab+c)t+ac-1=0,
∵t2-3t+1=0,
∴t2=3t-1,
于是上式可化为(3b+ab+c)t-b+ac-1=0
由于t是无理数,故有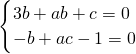
∵a,b是有理数,∵a2+3a+1≠0,由上面方程组解得:
b=-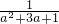 ,c=
,c=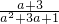
(2)因为x2+2=(3t-1)+2=3t+1=3(t+ ),
),
由(1)知,对a= ,有b=-
,有b=-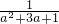 =-
=-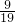 ,c=
,c=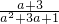 =
=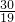 ,
,
使得(t+ )(-
)(-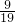 t+
t+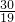 )=1,
)=1,
从而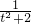 =
= (-
(-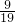 t+
t+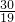 )=-
)=-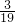 t+
t+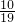 .
.
分析:(1)先求出t的值,再根据题意得到关于t的一元二次方程,代入已知方程(t+a)(bt+c)=1,可得到关于a、b、c的方程组,再用a表示出b、c的值即可;
(2)由(1)可把t2+2表示成3t+1的形式,再把a= 代入(1)中b、c的式子,可求出b、c的值,进而可把
代入(1)中b、c的式子,可求出b、c的值,进而可把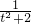 表示成dt+e的形式.
表示成dt+e的形式.
点评:本题难度较大,解答此题的关键是把t代入原方程,得到关于t的一元二次方程,用a表是出b、c的值.
 是无理数,
是无理数,由(t+a)(bt+c)=1得bt2+(ab+c)t+ac-1=0,
∵t2-3t+1=0,
∴t2=3t-1,
于是上式可化为(3b+ab+c)t-b+ac-1=0
由于t是无理数,故有
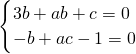
∵a,b是有理数,∵a2+3a+1≠0,由上面方程组解得:
b=-
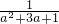 ,c=
,c=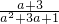
(2)因为x2+2=(3t-1)+2=3t+1=3(t+
 ),
),由(1)知,对a=
 ,有b=-
,有b=-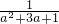 =-
=-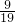 ,c=
,c=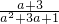 =
=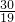 ,
,使得(t+
 )(-
)(-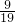 t+
t+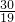 )=1,
)=1,从而
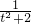 =
= (-
(-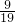 t+
t+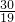 )=-
)=-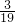 t+
t+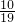 .
.分析:(1)先求出t的值,再根据题意得到关于t的一元二次方程,代入已知方程(t+a)(bt+c)=1,可得到关于a、b、c的方程组,再用a表示出b、c的值即可;
(2)由(1)可把t2+2表示成3t+1的形式,再把a=
 代入(1)中b、c的式子,可求出b、c的值,进而可把
代入(1)中b、c的式子,可求出b、c的值,进而可把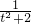 表示成dt+e的形式.
表示成dt+e的形式.点评:本题难度较大,解答此题的关键是把t代入原方程,得到关于t的一元二次方程,用a表是出b、c的值.

练习册系列答案
相关题目
 m=________.
m=________.