题目内容
【题目】如图，已知线段AB=12，点M、N是线段AB上的两点，且AM=BN=2，点P是线段MN上的动点，分别以线段AP、BP为边在AB的同侧作正方形APDC、正方形PBFE，点G、H分别是CD、EF的中点，点O是GH的中点，当P点从M点到N点运动过程中，OM+OB的最小值是（ ）
A.10B.12C.2 
D.12
【答案】C
【解析】
作点M关于直线XY的对称点M′，连接BM′，与XY交于点O，由轴对称性质可知，此时OM+OB=BM′最小，根据勾股定理即可求出BM'的值．
解：作点M关于直线XY的对称点M′，连接BM′，与XY交于点O．O′O″⊥A于O″B．GL⊥AB于L，HT⊥AB于T．
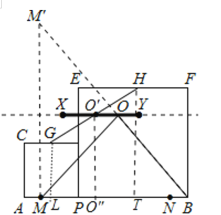
由轴对称性质可知，此时OM+OB=BM′最小（O′O″=
（GL+HT）=6），
在Rt△BMM′中，MM′=2O′O″=2×6=12，BM=10，
由勾股定理得：BM′=
=2
，
∴OM+OB的最小值为2，
故选：C．
练习册系列答案
相关题目
