题目内容
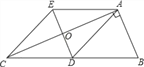
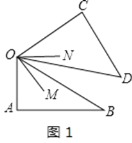
【题目】一副三角板AOB与COD如图摆放,且∠A=∠C=90°,∠AOB=60°,∠COD=45°,ON平分∠COB,OM平分∠AOD.当三角板COD绕O点顺时针旋转(从图1到图2).设图1、图2中的∠NOM的度数分别为α,β,![]() =______度.
=______度.
【答案】105
【解析】
图1中先设∠AOM=x=∠DOM,则∠BOM=60x,根据∠BOD=∠DOM∠BOM,得出∠BOD的度数,再根据∠COB=∠BOD+∠DOC,求出∠CON=∠BON,最后根据∠NOM=∠BOM+∠BON,即可得出α; 图2中设∠AOM=∠DOM=x,∠CON=∠BON=y,则∠BOD=602x,根据∠AOB=60°,∠COD=45°,列出算式,求出xy的度数,最后根据∠MON与各角之间的关系,
解:图1中设∠AOM=x=∠DOM,
∵∠AOB=60°,
∴∠BOM=60°x,
∵∠BOD=∠DOM∠BOM,
∴∠BOD=x(60°x)=2x60°,
∵∠COB=∠BOD+∠DOC,
∴∠COB=(2x60°)+45°=2x15°,
∴∠CON=∠BON=![]() (2x15°)=x7.5°,
(2x15°)=x7.5°,
∴α=∠NOM=∠BOM+∠BON=60°x+x7.5°=52.5°;
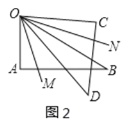
图2中设∠AOM=∠DOM=x,∠CON=∠BON=y,则∠BOD=60°2x,
∵∠COD=45°,
∴602x+2y=45°,即xy=7.5°,
∴β=∠MON=x+(602x)+y=60(xy)=52.5°,
∴![]() =52.5°+52.5°=105°,
=52.5°+52.5°=105°,
故答案为:105.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目