题目内容
设n=9+99+…+99…9(99个9).则n的十进制表示中,数码1有( )个.
| A.50 | B.90 | C.99 | D.100 |
C
由于9=10-1,99=100-1,…,所以n="9+99+999+…+"  =10+102+103+…1099-99×1.然后据此等式求出n的值后,即能得出n的十进制表示中,数码1有多少个.
=10+102+103+…1099-99×1.然后据此等式求出n的值后,即能得出n的十进制表示中,数码1有多少个.
解:n=9+99+999+…+
=10+102+103+…1099-99×1,
=1111111…10(99个1)-99,
=11111…1011(99个1).
所以在十进制表示中,数码1有99个.
故答案为:99.
根据式中数据的特点将式中的数据变为10的n次方相加的形式是完成本题的关键.
 =10+102+103+…1099-99×1.然后据此等式求出n的值后,即能得出n的十进制表示中,数码1有多少个.
=10+102+103+…1099-99×1.然后据此等式求出n的值后,即能得出n的十进制表示中,数码1有多少个.解:n=9+99+999+…+

=10+102+103+…1099-99×1,
=1111111…10(99个1)-99,
=11111…1011(99个1).
所以在十进制表示中,数码1有99个.
故答案为:99.
根据式中数据的特点将式中的数据变为10的n次方相加的形式是完成本题的关键.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
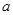 、
、 在数轴上对应点的位置如图所示,则必有 ( )
在数轴上对应点的位置如图所示,则必有 ( )


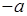 一定是一个负数;③没有绝对值为
一定是一个负数;③没有绝对值为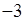 的数;④若
的数;④若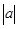 =a,则a是一个正数;⑤离原点左边越远的数就越小;正确的有( )个.
=a,则a是一个正数;⑤离原点左边越远的数就越小;正确的有( )个. 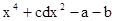 的值是 ;
的值是 ;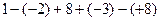 (2)
(2)
 (4)
(4)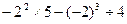
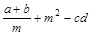 的值是 .
的值是 .