题目内容
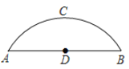
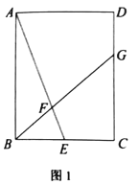
【题目】如图1,在矩形ABCD中,点E是BC的中点,点F是线段AE上一点,BF的延长线交CD于点G.
(1)若![]() ,则
,则![]() ______.
______.
(2)若![]() ,求
,求![]() 的值.(用含有m的代数式表示,写出解答过程)
的值.(用含有m的代数式表示,写出解答过程)
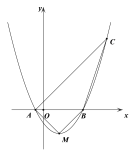
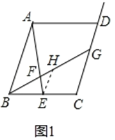
(3)如图2,四边形ABCD中,DC//AB,点E是BC的延长线上的一点,AE是BD相交于点F,若![]() ,
,![]() ,则
,则![]() ____.(直接用含a,b的代数式表示)
____.(直接用含a,b的代数式表示)
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3) ![]() .
.
【解析】
(1)如图1中,过点E作EH∥AB交BG于点H.由△ABF∽△EHF,推出![]() =
=![]() =3,推出AB=3EH,由四边形ABCD是平行四边形,EH∥AB,推出EH∥CD,AB=CD又E为BC中点,推出EH为△BCG的中位线,推出CG=2EH,即可推出
=3,推出AB=3EH,由四边形ABCD是平行四边形,EH∥AB,推出EH∥CD,AB=CD又E为BC中点,推出EH为△BCG的中位线,推出CG=2EH,即可推出![]() =
=![]() =
=![]() =
=![]() ;
;
(2)如图2中,作EH∥AB交BG于点H,则△EFH∽△AFB,推出![]() =
=![]() =a,推出AB=aEH,由AB=CD,推出CD=aEH,由EH∥AB∥CD,推出△BEH∽△BCG.推出
=a,推出AB=aEH,由AB=CD,推出CD=aEH,由EH∥AB∥CD,推出△BEH∽△BCG.推出![]() ,推出CG=2EH,推出DG=CD-CG=(a-2)EH,由此即可解决问题;
,推出CG=2EH,推出DG=CD-CG=(a-2)EH,由此即可解决问题;
(3)如图3中,过点E作EH∥AB交BD的延长线于点H,则有EH∥AB∥CD.由EH∥CD,推出△BCD∽△BEH,推出![]() =
=![]() =
=![]() ,推出CD=
,推出CD=![]() EH,又
EH,又![]() =a,推出AB=aCD=
=a,推出AB=aCD=![]() EH,由EH∥AB,推出△ABF∽△EHF,即可推出
EH,由EH∥AB,推出△ABF∽△EHF,即可推出![]() =
=![]() =
=![]() .
.
解:(1)如图1中,
过点E作EH∥AB交BG于点H.
则有△ABF∽△EHF,
∴![]() =
=![]() =3,
=3,
∴AB=3EH.
∵四边形ABCD是平行四边形,EH∥AB,
∴EH∥CD,AB=CD,
又∵E为BC中点,
∴EH为△BCG的中位线,
∴CG=2EH,
∴![]() =
=![]() =
=![]() =
=![]() .
.
故答案为![]() ;
;
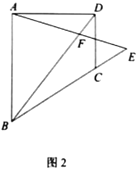
(2)解:如图所示,
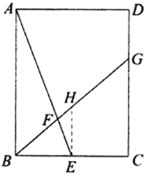
作EH∥AB交BG于点H,则△EFH∽△AFB.
∴![]() ,
,
∴AB=mEH.
∵AB=CD,
∴CD=mEH.
∵EH∥AB∥CD,
∴△BEH∽△BCG.
∴![]() ,
,
∴CG=2EH.
∴![]() .
.
(3)如图3所示,
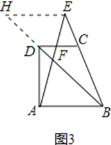
过点E作EH∥AB交BD的延长线于点H,则有EH∥AB∥CD.
∵EH∥CD,
∴△BCD∽△BEH,
∴![]() =
=![]() =
=![]() ,
,
∴CD=![]() EH.
EH.
又![]() =a ,
=a ,
∴AB=aCD=![]() EH.
EH.
∵EH∥AB,
∴△ABF∽△EHF,
∴![]() =
=![]() =
=![]() .
.
故答案为![]() .
.

【题目】良好的饮食对学生的身体、智力发育和健康起到了极其重要的作用,荤菜中蛋白质、钙、磷及脂溶性维生素优于素食,而素食中不饱和脂肪酸、维生素和纤维素又优于荤食,只有荤食与素食适当搭配,才能强化初中生的身体素质.某校为了了解学生的体质健康状况,以便食堂为学生提供合理膳食,对本校七年级、八年级学生的体质健康状况进行了调查,过程如下:
收集数据:从七、八年级两个年级中各抽取15名学生,进行了体质健康测试,测试成绩(百分制)如下:
七年级:74 81 75 76 70 75 75 79 81 70 74 80 91 69 82
八年级:81 94 83 77 83 80 81 70 81 73 78 82 80 70 50
整理数据:
年级 | x<60 | 60≤x<80 | 80≤x<90 | 90≤x≤100 |
七年级 | 0 | 10 | 4 | 1 |
八年级 | 1 | 5 | 8 | 1 |
(说明:90分及以上为优秀,80~90分(不含90分)为良好,60~80分(不含80分)为及格,60分以下为不及格)
分析数据:
年级 | 平均数 | 中位数 | 众数 |
七年级 |
| 75 | 75 |
八年级 | 77.5 | 80 |
|
得出结论:
(2)可以推断出 年级学生的体质健康状况更好一些,并说明理由;
(3)若七年级共有300名学生,请估计七年级体质健康成绩优秀的学生人数.
【题目】2018年平昌冬奥会在2月9日到25日在韩国平昌郡举行,为了调查中学生对冬奥会比赛项目的了解程度,某中学在学生中做了一次抽样调查,调查结果共分为四个等级:A、非常了解B、比较了解C、基本了解D、不了解.根据调查统计结果,绘制了如图所示的不完整的三种统计图表.
对冬奥会了解程度的统计表
对冬奥会的了解程度 | 百分比 |
A非常了解 | 10% |
B比较了解 | 15% |
C基本了解 | 35% |
D不了解 | n% |
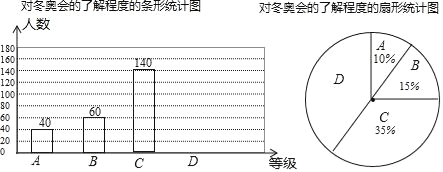
(1)n= ;
(2)扇形统计图中,D部分扇形所对应的圆心角是 ;
(3)请补全条形统计图;
(4)根据调查结果,学校准备开展冬奥会的知识竞赛,某班要从“非常了解”程度的小明和小刚中选一人参加,现设计了如下游戏来确定谁参赛,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4然后放到一个不透明的袋中,一个人先从袋中摸出一个球,另一人再从剩下的三个球中随机摸出一个球,若摸出的两个球上的数字和为偶数,则小明去,否则小刚去,请用画树状图或列表的方法说明这个游戏是否公平.