题目内容
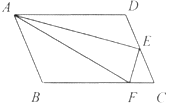
【题目】如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC,PF⊥CD,垂足分别为点E,F,连接AP,EF,给出下列四个结论:

①AP=EF;②∠PFE=∠BAP;③PD=![]() EC;④△APD一定是等腰三角形.
EC;④△APD一定是等腰三角形.
其中正确的结论有( ).
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】由四边形ABCD是正方形可以得出AB=BC=CD=AD,∠1=∠2=45°,作PH⊥AB于H,可以得出四边形BEPH为正方形,可以得出AH=CE,由条件可以得出四边形PECF是矩形,就有CE=PF,利用三角形全等可以得出AP=EF,∠PFE=∠BAP,由勾股定理可以得出PD=![]() PF,可以得出PD=
PF,可以得出PD=![]() EC,点P在BD上要使△APD一定是等腰三角只有AP=AD、PA=PD或DA=DP时才成立,故可以得出答案.
EC,点P在BD上要使△APD一定是等腰三角只有AP=AD、PA=PD或DA=DP时才成立,故可以得出答案.
作PH⊥AB于H,
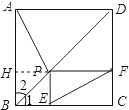
∴∠PHB=90°,
∵PE⊥BC,PF⊥CD,
∴∠PEB=∠PEC=∠PFC=90°.
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠1=∠2=∠BDC=45°,∠ABC=∠C=90°,
∴四边形BEPH和四边形PECF是矩形,PE=BE,DF=PF,
∴四边形BEPH为正方形,
∴BH=BE=PE=HP,
∴AH=CE,
∴△AHP≌△FPE,
∴AP=EF,∠PFE=∠BAP,
故①、②正确,
在Rt△PDF中,由勾股定理,得
PD=![]() PF,
PF,
∴PD=![]() CE.
CE.
故③正确.
∵点P在BD上,
∴当AP=AD、PA=PD或DA=DP时△APD是等腰三角形.
∴△APD是等腰三角形只有三种情况.
故④错误,
∴正确的个数有3个.
故选C.

练习册系列答案
相关题目