题目内容
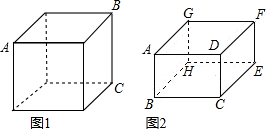 一只蚂蚁在立方体的表面积爬行.
一只蚂蚁在立方体的表面积爬行.(Ⅰ)如图1,当蚂蚁从正方体的一个顶点A沿表面爬行到顶点B,怎样爬行路线最短?说出你的理由.
(Ⅱ)如图1,如果蚂蚁要从边长为1cm的正方体的顶点A沿最短路线爬行到顶点C,那么爬行的最短距离d的长度应是下面选项中的( )
(A)1cm<l<3cm (B)2cm (C)3cm
这样的最短路径有
6
6
条.(Ⅲ)如果将正方体换成长AD=2cm,宽DF=2cm,高AB=1.5cm的长方体(如图2所示),蚂蚁仍需从顶点A沿表面爬行到顶点E的位置,请你说明这只蚂蚁沿怎样路线爬行距离最短?为什么?(可通过画图测量来说明)
分析:(I)根据线段的性质:两点之间线段最短,求出即可;
(II)根据图形可得出最短路径为
,进而得出答案即可;
(Ⅲ)将立方体采用两种不同的展开方式得出最短路径即可.
(II)根据图形可得出最短路径为
| 5 |
(Ⅲ)将立方体采用两种不同的展开方式得出最短路径即可.
解答: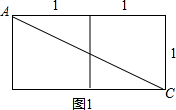 解:(I)如图1所示,沿线段AB爬行即可,根据两点之间线段最短;
解:(I)如图1所示,沿线段AB爬行即可,根据两点之间线段最短;
(II)如图2所示:1cm<l<3cm,
故选A,
路线有6条,如图2所示:

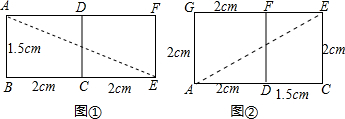
(III)蚂蚁爬行的最短路线是沿面AF和面FC展开后所连接的线段AE,
原因:如图①和图②所示作图,分别连接AE,并分别在两图中测量AE的长,可得图②中的AE较短.
也可利用勾股定理得出:图①中AE=
cm,图②中AE=
cm.
 解:(I)如图1所示,沿线段AB爬行即可,根据两点之间线段最短;
解:(I)如图1所示,沿线段AB爬行即可,根据两点之间线段最短;(II)如图2所示:1cm<l<3cm,
故选A,
路线有6条,如图2所示:

(III)蚂蚁爬行的最短路线是沿面AF和面FC展开后所连接的线段AE,
原因:如图①和图②所示作图,分别连接AE,并分别在两图中测量AE的长,可得图②中的AE较短.
也可利用勾股定理得出:图①中AE=
| ||
| 2 |
| ||
| 2 |

点评:本题考查了勾股定理的拓展应用.“化曲面为平面”是解决“怎样爬行最近”这类问题的关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
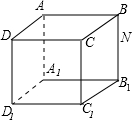 如图是一个棱长为4cm的正方体盒子,一只蚂蚁在D1C1的中点M处,它到BB1的中点N的最短路线是( )
如图是一个棱长为4cm的正方体盒子,一只蚂蚁在D1C1的中点M处,它到BB1的中点N的最短路线是( )| A、8 | ||
B、2
| ||
C、2
| ||
D、2+2
|
 如图,有一个高12cm,底面直径为10cm的圆锥,现有一只蚂蚁在圆锥的顶部M处,它想吃圆锥底部N处的食物,需要爬行的最短路程是
如图,有一个高12cm,底面直径为10cm的圆锥,现有一只蚂蚁在圆锥的顶部M处,它想吃圆锥底部N处的食物,需要爬行的最短路程是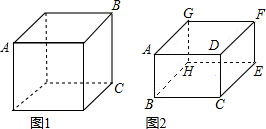 一只蚂蚁在立方体的表面积爬行.
一只蚂蚁在立方体的表面积爬行.