题目内容
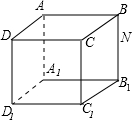 如图是一个棱长为4cm的正方体盒子,一只蚂蚁在D1C1的中点M处,它到BB1的中点N的最短路线是( )
如图是一个棱长为4cm的正方体盒子,一只蚂蚁在D1C1的中点M处,它到BB1的中点N的最短路线是( )| A、8 | ||
B、2
| ||
C、2
| ||
D、2+2
|
分析:把此正方体的DCC1D1面与CC1B1B面展开在同一平面内,然后利用勾股定理求点M和N点间的线段长,即可得到蚂蚁爬行的最短距离.在直角三角形MNB1中,一条直角边长等于6,另一条直角边长等于2,利用勾股定理可求得.
解答:解:把正方体的DCC1D1面与CC1B1B面展开在同一平面内,
∵M、N为C1D1和BB1的中点,
∴NB1=2,MC1=2,
在Rt△NMB1中,MN=
=2
.
故选C.
∵M、N为C1D1和BB1的中点,
∴NB1=2,MC1=2,
在Rt△NMB1中,MN=
| 22+62 |
| 10 |
故选C.
点评:本题考查了勾股定理的拓展应用.“化曲面为平面”是解决“怎样爬行最近”这类问题的关键.

练习册系列答案
相关题目
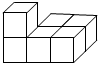 (2013•南平)如图是由六个棱长为1的正方体组成的一个几何体,其主视图的面积是( )
(2013•南平)如图是由六个棱长为1的正方体组成的一个几何体,其主视图的面积是( ) 如图,是一个边长为2的正方体,现有一只蚂蚁要从一条棱的中点A处沿正方体的表面到C处,则它爬行的最短线路长是( )
如图,是一个边长为2的正方体,现有一只蚂蚁要从一条棱的中点A处沿正方体的表面到C处,则它爬行的最短线路长是( ) 如图,是一个边长为2的正方体,现有一只蚂蚁要从一条棱的中点A处沿正方体的表面到C处,则它爬行的最短线路长是
如图,是一个边长为2的正方体,现有一只蚂蚁要从一条棱的中点A处沿正方体的表面到C处,则它爬行的最短线路长是

