题目内容
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 是线段
是线段![]() 上的点,
上的点,![]() 是线段
是线段![]() 上的点,且
上的点,且![]() .
.
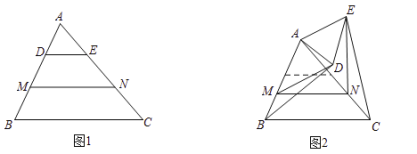
(1)观察猜想
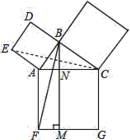
如图1,若点![]() 是线段
是线段![]() 的三等分点,则
的三等分点,则![]() __________,
__________,![]() ___________.由此,我们猜想线段
___________.由此,我们猜想线段![]() ,
,![]() ,
,![]() ,
,![]() 之间满足的数量关系是_________.
之间满足的数量关系是_________.
(2)类比探究
将![]() 在平面内绕点
在平面内绕点![]() 按逆时针方向旋转一定的角度,连接
按逆时针方向旋转一定的角度,连接![]() ,
,![]() ,
,![]() ,
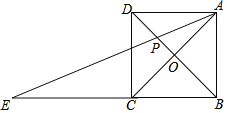
,![]() ,猜想在旋转的过程中,(1)中的结论是否仍然成立?若成立,请仅就图2的情形给出证明;若不成立,请说明理由.
,猜想在旋转的过程中,(1)中的结论是否仍然成立?若成立,请仅就图2的情形给出证明;若不成立,请说明理由.
(3)解决问题
将![]() 在平面内绕点
在平面内绕点![]() 自由旋转,若
自由旋转,若![]() ,请直接写出线段
,请直接写出线段![]() 的最大值.
的最大值.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)成立,证明详见解析;(3)
;(2)成立,证明详见解析;(3)![]() 的最大值为
的最大值为![]() .
.
【解析】
(1)根据三等分的定义求出比值即可,利用相似三角形的性质解决问题;
(2)证明△AMD∽△ANE,△ABD∽△ACE,利用相似三角形的性质解决问题即可;
(3)由(2)可知![]() ,求线段
,求线段![]() 的最大值,即为求线段
的最大值,即为求线段![]() 的最大值.
的最大值.
解:(1)∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)成立,证明如下:
由(1)可知![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
∴![]() ;
;
(3)由(2)可知![]() ,
,
∴求线段![]() 的最大值,即为求线段
的最大值,即为求线段![]() 的最大值,
的最大值,
由题意,可得![]() ,
,
在![]() 中,由三角形的三边关系,可得
中,由三角形的三边关系,可得![]() ,
,
∴当点![]() 共线时,
共线时,![]() ,即线段
,即线段![]() 的最大值为2,
的最大值为2,
∵![]() ,
,
把![]() 代入得
代入得![]() ,
,
∴线段![]() 的最大值为
的最大值为![]() .
.

 计算高手系列答案
计算高手系列答案【题目】为了实现伟大的强国复兴梦,全社会都在开展扫黑除恶专项斗争,某区为了解各学校老师对扫黑除恶应知应会知识的掌握情况,对甲、乙两个学校各180名老师进行了测试,从中各随机抽取30名教师的成绩(百分制),并对成绩(单位:分)进行整理、描述和分析,给出了部分成绩信息.

甲校参与测试的老师成绩在96≤x<98这一组的数据是:96,96.5,97,97.5,97,96.5,97.5,96,96.5,96.5,甲、乙两校参与测试的老师成绩的平均数、中位数、众数如下表:
学校 | 平均数 | 中位数 | 众数 |
甲校 | 96.35 | m | 99 |
乙校 | 95.85 | 97.5 | 99 |
根据以上信息,回答下列问题:
(1)m=________;
(2)在此次随机抽样测试中,甲校的王老师和乙校的李老师成绩均为97分,则他们在各自学校参与测试的老师中成绩的名次相比较更靠前的是________(选填王或李)老师,请写出理由;
(3)在此次随机测试中,乙校96分以上(含96分)的总人数比甲校96分以上(含96分)的总人数的2倍少100人,试估计乙校96分以上(含96分)的总人数.